What Is The Least Common Multiple Of 36 And 54
News Co
Mar 31, 2025 · 5 min read
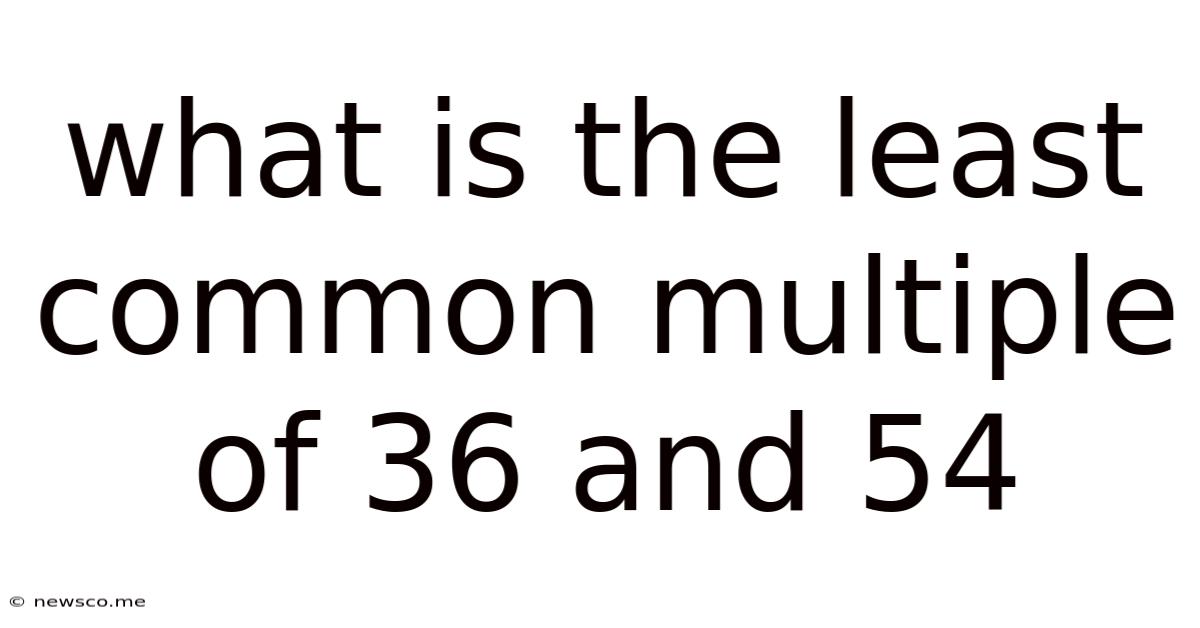
Table of Contents
What is the Least Common Multiple (LCM) of 36 and 54? A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem like a simple arithmetic problem, but understanding its underlying principles unlocks a deeper appreciation of number theory and its applications in various fields. This comprehensive guide will not only answer the question of what the LCM of 36 and 54 is but will also explore different methods for calculating it, delve into its significance, and explore related concepts.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the integers as factors. It's a fundamental concept in mathematics with applications ranging from simplifying fractions to scheduling events and solving problems in various fields like engineering and music theory.
Methods for Finding the LCM of 36 and 54
There are several ways to determine the LCM of 36 and 54. Let's explore the most common methods:
1. Listing Multiples Method
This is the most straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 36: 36, 72, 108, 144, 180, 216, 252, 288, 324, 360...
- Multiples of 54: 54, 108, 162, 216, 270, 324, 378, 432...
Notice that 108 appears in both lists. However, a smaller common multiple, 108, exists. Continuing, we find that 216 is also a common multiple. The smallest common multiple is 108.
This method is simple but becomes less efficient as the numbers get larger.
2. Prime Factorization Method
This method is more efficient for larger numbers. We start by finding the prime factorization of each number.
- Prime factorization of 36: 2² x 3² (36 = 2 x 2 x 3 x 3)
- Prime factorization of 54: 2 x 3³ (54 = 2 x 3 x 3 x 3)
Now, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2²
- Highest power of 3: 3³
Multiply these highest powers together: 2² x 3³ = 4 x 27 = 108
Therefore, the LCM of 36 and 54 is 108.
This method is generally preferred for its efficiency, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD). The product of the LCM and GCD of two numbers is equal to the product of the two numbers.
First, let's find the GCD of 36 and 54 using the Euclidean algorithm:
- Divide 54 by 36: 54 = 1 x 36 + 18
- Divide 36 by the remainder 18: 36 = 2 x 18 + 0
The GCD is the last non-zero remainder, which is 18.
Now, we can use the formula:
LCM(a, b) = (a x b) / GCD(a, b)
LCM(36, 54) = (36 x 54) / 18 = 1944 / 18 = 108
This method is also efficient and demonstrates the interconnectedness of LCM and GCD.
Significance of the Least Common Multiple
The LCM finds practical applications in numerous scenarios:
-
Fraction Addition and Subtraction: To add or subtract fractions with different denominators, you need to find the LCM of the denominators to create a common denominator. This simplifies the process and ensures accuracy.
-
Scheduling: Imagine two events repeating at different intervals. The LCM helps determine when both events will occur simultaneously. For example, if one event occurs every 36 days and another every 54 days, they will coincide again after 108 days.
-
Gear Ratios: In mechanical engineering, LCM is crucial for designing gear systems with specific ratios and synchronizing rotational speeds.
-
Music Theory: LCM is used in music to calculate the least common denominator of note durations, enabling the creation of harmonious and rhythmically consistent compositions.
-
Modular Arithmetic: LCM plays a vital role in solving problems related to modular arithmetic, which has applications in cryptography and computer science.
Further Exploration of Number Theory Concepts
Understanding the LCM leads to a deeper appreciation of several related concepts in number theory:
-
Greatest Common Divisor (GCD): As demonstrated earlier, the GCD and LCM are intimately related. Understanding their relationship is key to solving various number theory problems.
-
Prime Numbers: The prime factorization method for finding the LCM highlights the importance of prime numbers as the building blocks of all integers.
-
Euclidean Algorithm: This algorithm provides an efficient way to calculate the GCD, which, as we saw, is crucial for calculating the LCM.
-
Modular Arithmetic: The LCM is used extensively in modular arithmetic, which is a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus).
Conclusion: The LCM of 36 and 54 and Beyond
We've definitively established that the least common multiple of 36 and 54 is 108. However, the journey to this answer has revealed much more than just a numerical result. We've explored various methods for calculating the LCM, highlighting their strengths and weaknesses. More importantly, we've uncovered the significance of the LCM in diverse fields and its connection to fundamental concepts in number theory. Understanding the LCM is not just about solving a mathematical problem; it's about appreciating the elegant interconnectedness of mathematical ideas and their practical applications in the world around us. This deep dive into the LCM of 36 and 54 serves as a gateway to further exploration of number theory and its fascinating world of patterns, relationships, and applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 36 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.