What Is The Least Common Multiple Of 6 And 16
News Co
Mar 15, 2025 · 5 min read
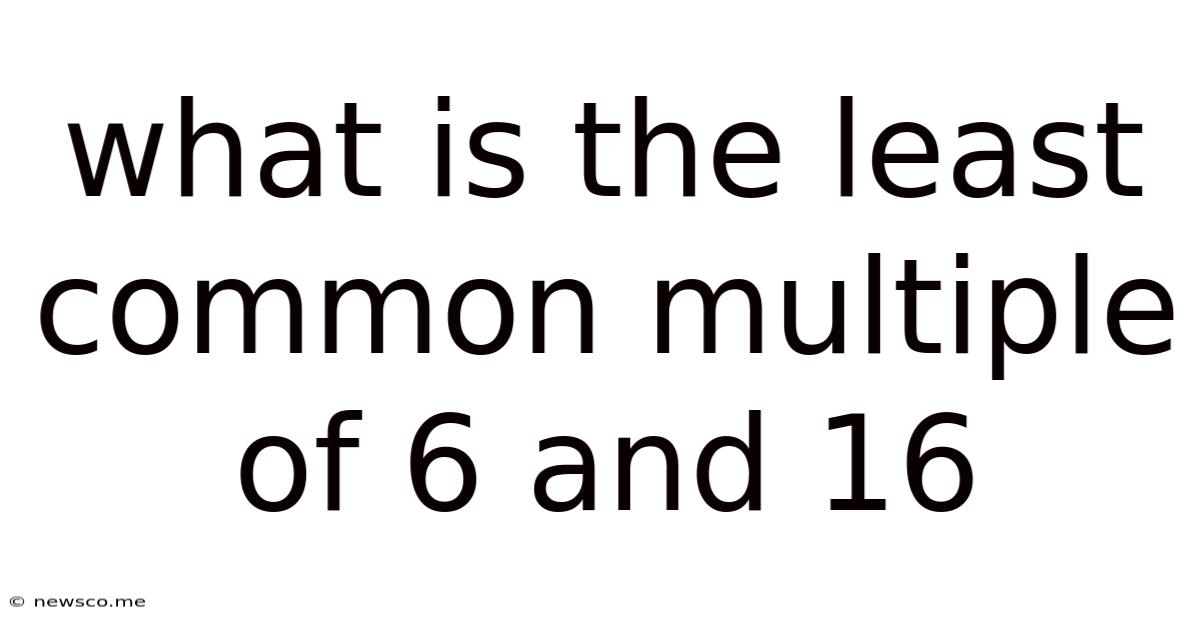
Table of Contents
What is the Least Common Multiple (LCM) of 6 and 16? A Deep Dive into Finding LCMs
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex problems in algebra and number theory. This article will delve into the process of determining the LCM of 6 and 16, exploring multiple methods, explaining the underlying principles, and providing a broader understanding of LCMs within the context of number theory.
Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's essentially the smallest number that contains all the integers as factors. This concept is distinct from the greatest common divisor (GCD), which is the largest integer that divides both numbers without leaving a remainder. While seemingly separate, LCM and GCD are intimately related, as we'll see later.
Methods for Finding the LCM of 6 and 16
Several methods exist for calculating the LCM, each offering a unique approach and level of understanding. Let's explore the most common techniques:
1. Listing Multiples Method
This is a straightforward, intuitive method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
- Multiples of 16: 16, 32, 48, 64, 80, 96, ...
By comparing the lists, we observe that the smallest common multiple is 48. Therefore, the LCM(6, 16) = 48.
This method is simple but becomes less efficient as the numbers increase in size. Imagine trying this with larger numbers like 144 and 288; the list of multiples would become incredibly long.
2. Prime Factorization Method
This is a more efficient and systematic method, especially for larger numbers. It relies on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Step 1: Prime Factorization
Let's find the prime factorization of 6 and 16:
- 6 = 2 x 3
- 16 = 2 x 2 x 2 x 2 = 2<sup>4</sup>
Step 2: Identify Common and Uncommon Prime Factors
We identify the prime factors present in both numbers and the unique prime factors:
- Common prime factor: 2
- Uncommon prime factors: 3 and an additional 2<sup>3</sup> (from 16)
Step 3: Calculate the LCM
To find the LCM, we take the highest power of each prime factor present in the factorizations and multiply them together:
LCM(6, 16) = 2<sup>4</sup> x 3 = 16 x 3 = 48
This method is generally preferred for its efficiency and scalability, making it suitable for larger numbers.
3. Using the GCD (Greatest Common Divisor)
The LCM and GCD are intimately related through the following formula:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
First, we need to find the GCD of 6 and 16. Using the Euclidean algorithm (a simple and efficient method for finding the GCD):
- Divide the larger number (16) by the smaller number (6): 16 ÷ 6 = 2 with a remainder of 4.
- Replace the larger number with the smaller number (6) and the smaller number with the remainder (4): 6 ÷ 4 = 1 with a remainder of 2.
- Repeat: 4 ÷ 2 = 2 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 2.
Now, we can apply the formula:
LCM(6, 16) = (6 x 16) / GCD(6, 16) = 96 / 2 = 48
This method elegantly connects the LCM and GCD, demonstrating their inherent relationship. It's particularly useful when the GCD is readily available or easily calculated.
Applications of LCM
The concept of LCM extends far beyond simple arithmetic exercises. It plays a vital role in various mathematical and real-world scenarios:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Cyclic Events: Determining when events that repeat at different intervals will coincide (e.g., two planets aligning, machines needing maintenance simultaneously).
- Scheduling Problems: Optimizing schedules and planning tasks with different repeating cycles.
- Number Theory: LCMs are fundamental in many number theory concepts, including modular arithmetic and solving Diophantine equations.
- Computer Science: LCM calculations are used in algorithms related to scheduling, synchronization, and data structures.
Expanding the Concept: LCM of More Than Two Numbers
The methods discussed can be extended to find the LCM of more than two numbers. The prime factorization method remains the most efficient. For instance, let's find the LCM of 6, 16, and 20:
-
Prime Factorization:
- 6 = 2 x 3
- 16 = 2<sup>4</sup>
- 20 = 2<sup>2</sup> x 5
-
Identify highest powers of prime factors: 2<sup>4</sup>, 3, 5
-
Calculate LCM: LCM(6, 16, 20) = 2<sup>4</sup> x 3 x 5 = 16 x 3 x 5 = 240
Conclusion: The Significance of LCM in Mathematics and Beyond
The least common multiple, seemingly a simple concept, is a cornerstone of number theory and has far-reaching applications in various fields. Understanding the different methods for calculating the LCM, especially the prime factorization method, equips you with a powerful tool for solving a range of mathematical problems and tackling real-world challenges involving repetitive cycles or rhythmic patterns. The relationship between LCM and GCD further enriches our understanding of the fundamental building blocks of number theory. The LCM of 6 and 16, determined to be 48 through multiple methods, serves as a clear example of this foundational concept, illustrating its power and versatility within the realm of mathematics and its practical applications. Mastering the concept of LCM is an essential step in advancing mathematical understanding and problem-solving capabilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 6 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.