What Is The Least Common Multiple Of 6 And 24
News Co
Apr 03, 2025 · 5 min read
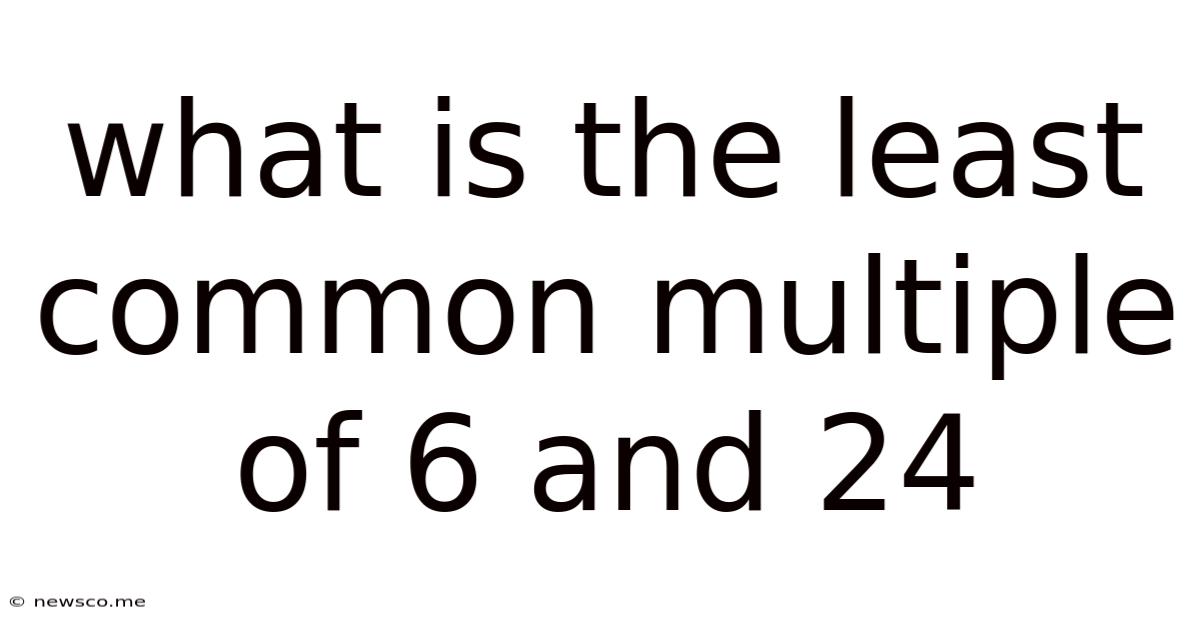
Table of Contents
What is the Least Common Multiple (LCM) of 6 and 24? A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the concept thoroughly opens doors to more complex mathematical concepts. This article will not only answer the question "What is the least common multiple of 6 and 24?" but also explore the underlying principles, different methods of calculation, and its applications in various fields.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
It's crucial to distinguish LCM from the greatest common divisor (GCD). The GCD is the largest positive integer that divides each of the integers without leaving a remainder. While both concepts deal with divisibility, they provide different, yet complementary, information about the relationships between numbers.
Calculating the LCM of 6 and 24: Three Proven Methods
Now, let's tackle the specific question: what is the LCM of 6 and 24? We'll explore three common methods to determine this:
Method 1: Listing Multiples
The most straightforward method is listing the multiples of each number until a common multiple is found.
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 24: 24, 48, 72...
The smallest number that appears in both lists is 24. Therefore, the LCM of 6 and 24 is 24.
This method works well for smaller numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers.
-
Find the prime factorization of each number:
- 6 = 2 x 3
- 24 = 2 x 2 x 2 x 3 = 2³ x 3
-
Identify the highest power of each prime factor:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
-
Multiply the highest powers together:
- LCM(6, 24) = 2³ x 3 = 8 x 3 = 24
This method is more efficient than listing multiples, especially for larger numbers, as it directly identifies the essential components of the LCM.
Method 3: Using the Formula LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the relationship between the LCM and the greatest common divisor (GCD). First, we need to find the GCD of 6 and 24.
-
Find the GCD of 6 and 24:
- Factors of 6: 1, 2, 3, 6
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- The greatest common factor is 6. Therefore, GCD(6, 24) = 6.
-
Apply the formula:
- LCM(6, 24) = (6 x 24) / 6 = 24
This method requires calculating the GCD first, but it provides a concise formula for calculating the LCM, especially useful when dealing with larger numbers where prime factorization might become more complex.
Applications of LCM in Real-World Scenarios
The concept of LCM might seem abstract, but it has practical applications in various fields:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 6 minutes, and the other every 24 minutes. The LCM helps determine when both buses will arrive simultaneously, which is crucial for scheduling and coordination. In this case, they will arrive together every 24 minutes.
-
Fraction Operations: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators. For example, adding 1/6 and 1/24 requires finding the LCM of 6 and 24 (which is 24), allowing you to rewrite the fractions with a common denominator for easy addition.
-
Gear Ratios: In mechanical engineering, LCM plays a role in calculating gear ratios and optimizing the synchronization of rotating parts in machinery. Understanding the least common multiple ensures smooth and efficient operation.
-
Cyclic Events: Many real-world phenomena exhibit cyclical behavior. LCM can be used to predict when these cycles align. For instance, in astronomy, calculating the time when planets align requires understanding the LCM of their orbital periods.
-
Project Management: When managing projects with tasks that repeat at different intervals, the LCM helps determine the timing for recurring meetings or reviews, ensuring optimal efficiency and resource allocation.
Beyond the Basics: LCM for More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly effective in these situations. For example, to find the LCM of 6, 24, and 12:
-
Prime Factorization:
- 6 = 2 x 3
- 24 = 2³ x 3
- 12 = 2² x 3
-
Highest Powers:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
-
Multiplication:
- LCM(6, 24, 12) = 2³ x 3 = 8 x 3 = 24
Therefore, the LCM of 6, 24, and 12 is 24.
Conclusion: Mastering the LCM for Mathematical Proficiency
Understanding the least common multiple is not just about solving simple arithmetic problems; it's about grasping a fundamental concept with wide-ranging applications. The three methods discussed—listing multiples, prime factorization, and using the LCM/GCD relationship—offer diverse approaches to calculating the LCM, each with its advantages depending on the context and the numbers involved. By mastering these techniques, you'll enhance your mathematical skills and gain a deeper appreciation for the intricate beauty of number theory and its relevance in solving real-world challenges. Remember to choose the method that best suits your needs and the complexity of the numbers you're working with. The ability to efficiently calculate the LCM is a valuable tool in many areas, from everyday tasks to complex scientific and engineering problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 6 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.