What Is The Least Common Multiple Of 9 And 2
News Co
Apr 06, 2025 · 5 min read
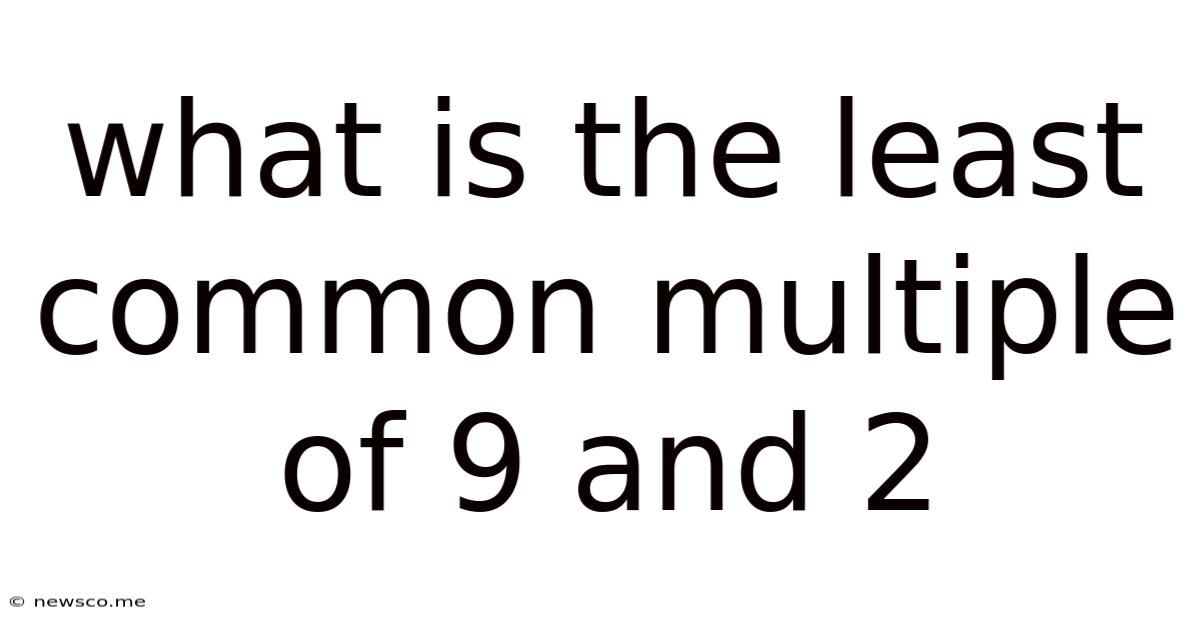
Table of Contents
What is the Least Common Multiple (LCM) of 9 and 2? A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple task, especially for small numbers like 9 and 2. However, understanding the underlying concepts and methods involved is crucial for tackling more complex problems in number theory and various applications in mathematics and computer science. This article will not only answer the question – what is the LCM of 9 and 2? – but will also explore the different ways to calculate the LCM, delve into its significance, and touch upon its real-world applications.
Understanding the Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that is divisible by all the given numbers without leaving a remainder. For example, the LCM of 4 and 6 is 12, because 12 is the smallest positive integer that is divisible by both 4 and 6.
Distinguishing LCM from Greatest Common Divisor (GCD)
It's important to differentiate the LCM from the greatest common divisor (GCD), also known as the greatest common factor (GCF). The GCD is the largest positive integer that divides each of the given integers without leaving a remainder. For instance, the GCD of 4 and 6 is 2. While both LCM and GCD are fundamental concepts in number theory, they represent different aspects of the relationship between numbers.
Calculating the LCM of 9 and 2: Methods and Approaches
Now, let's address the core question: what is the LCM of 9 and 2? We can employ several methods to calculate this.
Method 1: Listing Multiples
The simplest method is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
By examining the lists, we observe that the smallest number appearing in both lists is 18. Therefore, the LCM of 9 and 2 is 18.
Method 2: Prime Factorization
This method is more efficient for larger numbers. We find the prime factorization of each number and then construct the LCM using the highest powers of all prime factors present in either factorization.
- Prime factorization of 9: 3²
- Prime factorization of 2: 2¹
The LCM is constructed by taking the highest power of each prime factor: 2¹ * 3² = 2 * 9 = 18. Therefore, the LCM of 9 and 2 is 18.
Method 3: Using the Formula relating LCM and GCD
There's a useful formula that relates the LCM and GCD of two numbers:
LCM(a, b) * GCD(a, b) = a * b
First, we find the GCD of 9 and 2. Since 9 and 2 have no common factors other than 1, their GCD is 1.
Now, we can use the formula:
LCM(9, 2) * GCD(9, 2) = 9 * 2
LCM(9, 2) * 1 = 18
LCM(9, 2) = 18
This confirms that the LCM of 9 and 2 is 18.
The Significance of LCM in Mathematics and Beyond
The LCM is not just a theoretical concept; it has significant practical applications across various fields.
Applications in Mathematics
-
Fraction Addition and Subtraction: Finding the LCM of the denominators is essential when adding or subtracting fractions. This allows us to find a common denominator, simplifying the calculation.
-
Solving Diophantine Equations: LCM plays a crucial role in solving Diophantine equations, which are equations where only integer solutions are sought.
-
Modular Arithmetic: LCM finds application in modular arithmetic, a branch of number theory concerning remainders after division.
Applications in Real-World Scenarios
-
Scheduling Problems: Imagine you have two machines that perform cycles of 9 and 2 hours respectively. Finding the LCM (18 hours) determines when both machines will simultaneously complete a cycle. This is fundamental in scheduling repetitive tasks.
-
Gear Ratios: In mechanical engineering, the LCM is used in determining gear ratios to ensure smooth and efficient power transmission.
-
Music Theory: In music, the LCM is used to calculate the least common multiple of the frequencies of different musical notes, which helps in understanding harmonies and intervals.
-
Construction and Engineering: LCM is essential for projects involving repetitive tasks or patterns, such as tiling, flooring, or designing structural elements. Ensuring harmonious patterns often requires finding the LCM of different dimensions.
Further Exploration: LCM of More Than Two Numbers
The concept of LCM extends to more than two numbers. For instance, to find the LCM of 9, 2, and 6, we can again use the prime factorization method.
- Prime factorization of 9: 3²
- Prime factorization of 2: 2¹
- Prime factorization of 6: 2¹ * 3¹
The LCM will be 2¹ * 3² = 18.
Alternatively, we could find the LCM of 9 and 2 (18), and then find the LCM of 18 and 6, which is also 18.
Conclusion: The LCM of 9 and 2 and its Broader Implications
The least common multiple of 9 and 2 is definitively 18. While this specific calculation might seem trivial, understanding the underlying principles and different methods for calculating the LCM is invaluable. The LCM is a fundamental concept with far-reaching implications in various branches of mathematics and numerous real-world applications. By mastering this seemingly simple concept, you unlock a powerful tool for solving complex problems and gaining a deeper appreciation for the beauty and practicality of number theory. The techniques discussed – listing multiples, prime factorization, and the LCM/GCD relationship – provide a comprehensive toolkit for tackling LCM calculations regardless of the numbers involved. Remember, the key is to understand the underlying mathematical principles, which then allows you to apply them effectively in different contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 9 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.