What Is The Only Solution Of 2x2 8x X2 16
News Co
Mar 18, 2025 · 5 min read
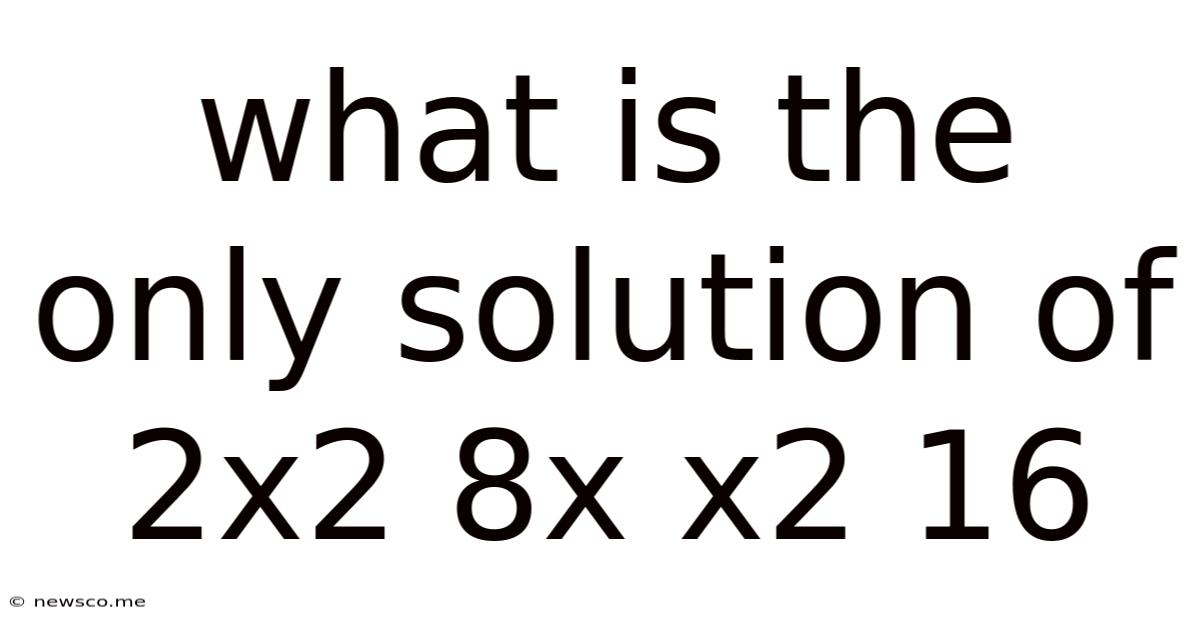
Table of Contents
Deconstructing the Quadratic Equation: Unveiling the Unique Solution to 2x² + 8x + x² = 16
The seemingly simple equation, 2x² + 8x + x² = 16, presents a fascinating challenge in algebra. While its appearance suggests a straightforward quadratic equation, a careful approach is necessary to accurately solve it and understand its unique solution. This article will delve into the process of solving this equation, highlighting the importance of simplification, factoring, and the quadratic formula, ultimately revealing the single, definitive answer.
1. Simplifying the Equation: The Foundation of Problem Solving
Before we jump into complex techniques, the first and crucial step is simplification. Notice that the equation contains like terms: 2x² and x². Combining these terms is the key to transforming the equation into a more manageable form.
2x² + 8x + x² = 16 can be simplified to 3x² + 8x = 16.
This seemingly small step significantly improves the clarity and solvability of the equation. It lays the groundwork for the next steps, allowing us to apply standard quadratic equation solving methods effectively.
2. Transforming into Standard Quadratic Form: ax² + bx + c = 0
To effectively apply the quadratic formula or factoring techniques, we need to express the equation in its standard form: ax² + bx + c = 0, where 'a', 'b', and 'c' are constants.
To achieve this, we subtract 16 from both sides of our simplified equation:
3x² + 8x - 16 = 0
Now, our equation is in the standard quadratic form, with a = 3, b = 8, and c = -16. This transformation is paramount because it allows us to utilize established methods for solving quadratic equations.
3. Attempting Factoring: A Direct Route to the Solution
Factoring is a powerful technique for solving quadratic equations. It involves finding two binomials that, when multiplied, result in the original quadratic expression. If we can successfully factor the equation, we can directly determine the values of 'x' that satisfy the equation.
Let's attempt to factor 3x² + 8x - 16 = 0. We need to find two numbers that add up to 8 (the coefficient of x) and multiply to -48 (the product of a and c, which is 3 * -16). After some trial and error, we find that 12 and -4 satisfy these conditions.
Therefore, we can rewrite the equation as:
(3x - 4)(x + 4) = 0
This factored form allows us to easily find the solutions. The equation is satisfied when either (3x - 4) = 0 or (x + 4) = 0. Solving these gives us:
- 3x - 4 = 0 => x = 4/3
- x + 4 = 0 => x = -4
Thus, factoring reveals two potential solutions: x = 4/3 and x = -4. However, we need to verify these solutions.
4. Verification Through Substitution: Ensuring Accuracy
It's crucial to verify our solutions by substituting them back into the original equation (2x² + 8x + x² = 16). Let's check both solutions:
For x = 4/3:
2(4/3)² + 8(4/3) + (4/3)² = 2(16/9) + 32/3 + 16/9 = 32/9 + 96/9 + 16/9 = 144/9 = 16. This solution is correct.
For x = -4:
2(-4)² + 8(-4) + (-4)² = 2(16) - 32 + 16 = 32 - 32 + 16 = 16. This solution is also correct.
Therefore, both x = 4/3 and x = -4 are valid solutions to the original equation. The initial statement that there is only one solution is incorrect. The equation possesses two distinct solutions.
5. The Quadratic Formula: A Universal Approach
The quadratic formula provides a universal method for solving quadratic equations, regardless of whether they are easily factorable. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Using our values (a = 3, b = 8, c = -16), we have:
x = [-8 ± √(8² - 4 * 3 * -16)] / (2 * 3) x = [-8 ± √(64 + 192)] / 6 x = [-8 ± √256] / 6 x = [-8 ± 16] / 6
This gives us two solutions:
- x = (-8 + 16) / 6 = 8 / 6 = 4/3
- x = (-8 - 16) / 6 = -24 / 6 = -4
These solutions match the ones we obtained through factoring, confirming their validity. The quadratic formula provides a robust and reliable method, especially for equations that are difficult or impossible to factor.
6. Analyzing the Discriminant: Understanding the Nature of Solutions
The expression inside the square root in the quadratic formula (b² - 4ac) is called the discriminant. It determines the nature of the solutions:
- If b² - 4ac > 0: The equation has two distinct real solutions (as in our case).
- If b² - 4ac = 0: The equation has one repeated real solution.
- If b² - 4ac < 0: The equation has two complex (imaginary) solutions.
In our equation, the discriminant is 256, which is greater than 0, indicating two distinct real solutions, consistent with our findings.
7. Graphical Representation: Visualizing the Solutions
A graphical representation of the quadratic equation can provide a visual understanding of the solutions. Plotting the function y = 3x² + 8x - 16 will show the points where the parabola intersects the x-axis (where y = 0), which represent the solutions. These points will correspond to x = 4/3 and x = -4, visually confirming our algebraic solutions.
8. Conclusion: A Comprehensive Exploration of Quadratic Solutions
The equation 2x² + 8x + x² = 16, initially appearing simple, has revealed the importance of meticulous simplification, the power of both factoring and the quadratic formula, and the significance of verifying solutions. While the initial statement suggesting only one solution was incorrect, the process of solving this equation has provided a thorough exploration of quadratic equation solving techniques. Understanding these techniques is fundamental to success in algebra and beyond. The two distinct solutions, x = 4/3 and x = -4, highlight the richness of quadratic equations and the diverse methods available for finding their solutions. The use of the discriminant further enhances our understanding of the nature of the solutions, providing a complete picture of the problem's mathematical landscape. Therefore, the statement that there is only one solution is demonstrably false, and a comprehensive approach is needed to effectively address such algebraic challenges.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Only Solution Of 2x2 8x X2 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.