What Is The Percent Of 3 10
News Co
Apr 02, 2025 · 5 min read
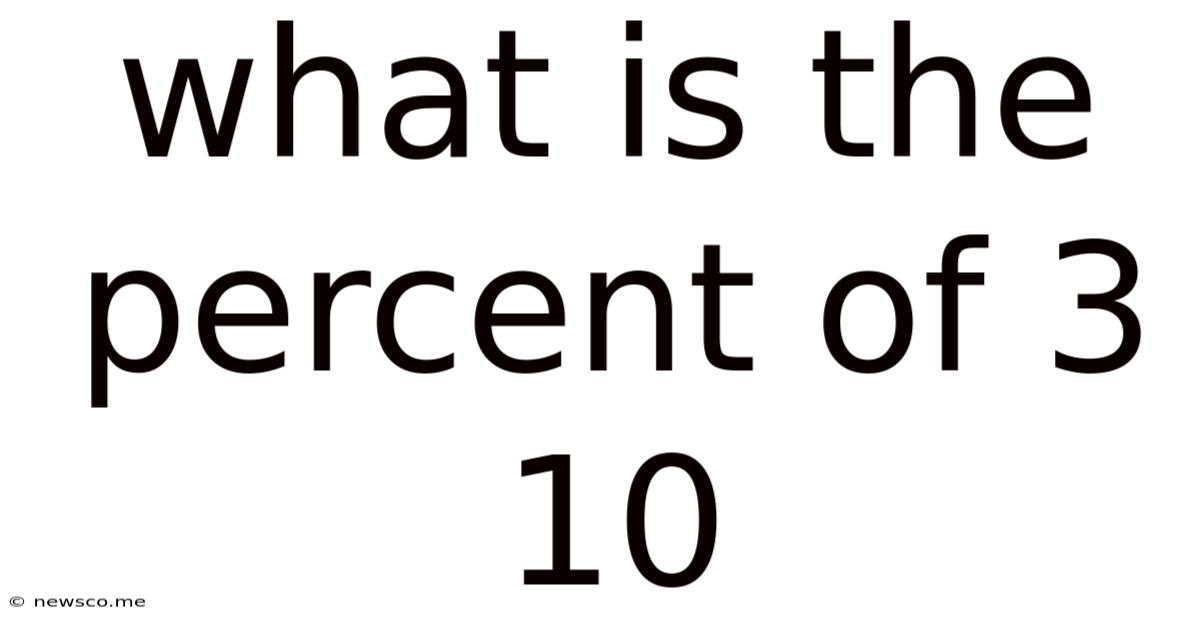
Table of Contents
What is the Percent of 3/10? Understanding Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill in mathematics and everyday life. This article will thoroughly explain how to convert the fraction 3/10 into a percentage, providing a step-by-step guide and exploring the broader context of these mathematical concepts. We'll also delve into practical applications and address common misconceptions.
From Fraction to Percentage: A Step-by-Step Guide
The fraction 3/10 represents three parts out of a total of ten equal parts. To convert this fraction to a percentage, we need to express it as a number out of 100. Here's the process:
1. Understanding the Relationship:
A percentage is simply a fraction where the denominator is 100. The symbol "%" represents "per hundred" or "out of 100." Therefore, converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100.
2. Converting 3/10 to a Percentage:
-
Method 1: Direct Conversion: Since 10 multiplied by 10 equals 100, we can easily convert 3/10 to a percentage by multiplying both the numerator and the denominator by 10:
(3 x 10) / (10 x 10) = 30/100
Therefore, 3/10 is equivalent to 30%.
-
Method 2: Decimal Conversion: First, convert the fraction 3/10 to a decimal by performing the division:
3 ÷ 10 = 0.3
Then, multiply the decimal by 100 to express it as a percentage:
0.3 x 100 = 30%
Again, we find that 3/10 is equal to 30%.
Deep Dive into Fractions, Decimals, and Percentages
Let's explore each of these mathematical concepts in more detail to solidify your understanding:
Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts being considered, and the denominator indicates the total number of equal parts that make up the whole. For example, in the fraction 3/10, 3 is the numerator and 10 is the denominator.
Types of Fractions:
- Proper Fractions: The numerator is smaller than the denominator (e.g., 3/10, 1/2).
- Improper Fractions: The numerator is larger than or equal to the denominator (e.g., 7/5, 4/4).
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 2 1/3).
Decimals: Representing Fractions in Base 10
Decimals are another way of representing fractions. They use a base-10 system, where each place value to the right of the decimal point represents a power of 10 (tenths, hundredths, thousandths, and so on). For example, 0.3 represents three-tenths (3/10), and 0.30 represents thirty-hundredths (30/100), which is equivalent to 3/10.
Percentages: Expressing Fractions as Parts of 100
Percentages are a special type of fraction where the denominator is always 100. They are often used to express proportions, rates, or changes. The percentage symbol (%) is used to represent "per hundred." For instance, 30% means 30 out of 100.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is crucial in various aspects of daily life, including:
- Finance: Calculating interest rates, discounts, taxes, tips, and profit margins.
- Shopping: Determining sale prices, comparing deals, and understanding value.
- Science: Representing experimental data, expressing concentrations, and calculating statistical probabilities.
- Everyday Life: Interpreting survey results, understanding statistics in news reports, and calculating proportions in recipes.
Common Mistakes to Avoid When Working with Percentages
Several common errors can lead to incorrect percentage calculations. Be mindful of these to ensure accuracy:
- Confusing Percentage and Decimal: Remember to multiply the decimal by 100 when converting to a percentage, and divide by 100 when converting from a percentage to a decimal.
- Incorrectly Calculating Percentage Increase or Decrease: Percentage change calculations require a slightly different approach. Make sure to calculate the difference between the original and new value, then divide by the original value before multiplying by 100.
- Improper Use of Percentages in Comparisons: Avoid comparing percentages without considering the base values. A seemingly larger percentage increase may not necessarily be more significant if the base values differ significantly.
- Misinterpreting Percentage Points: Percentage points refer to the arithmetic difference between two percentages. For example, an increase from 20% to 25% is a 5 percentage point increase, not a 25% increase.
Expanding Your Understanding: Beyond 3/10
While we've focused on the specific example of 3/10, the principles discussed are applicable to converting any fraction to a percentage. Practice converting various fractions to strengthen your understanding. For example, try converting fractions such as 1/4, 2/5, 7/8, and even improper fractions like 5/2 into percentages using the methods described above. This practice will help you develop fluency and confidence in working with these essential mathematical concepts.
Conclusion: Mastering the Fundamentals
Understanding how to calculate percentages is a valuable skill that has wide-ranging applications in various aspects of life. By grasping the relationship between fractions, decimals, and percentages, you can tackle a broad range of mathematical problems and make informed decisions in your daily life. Remember to practice regularly, be mindful of common mistakes, and continue to explore the applications of these fundamental concepts. With consistent practice and attention to detail, you can master the art of percentage calculations and use them effectively in your personal and professional endeavors. Remember, the key is understanding the underlying principles, not just memorizing formulas. By focusing on the "why" behind the calculations, you'll build a solid foundation that will serve you well in your mathematical journey.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Percent Of 3 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.