What Is The Percentage Of 10 Out Of 15
News Co
Apr 15, 2025 · 5 min read
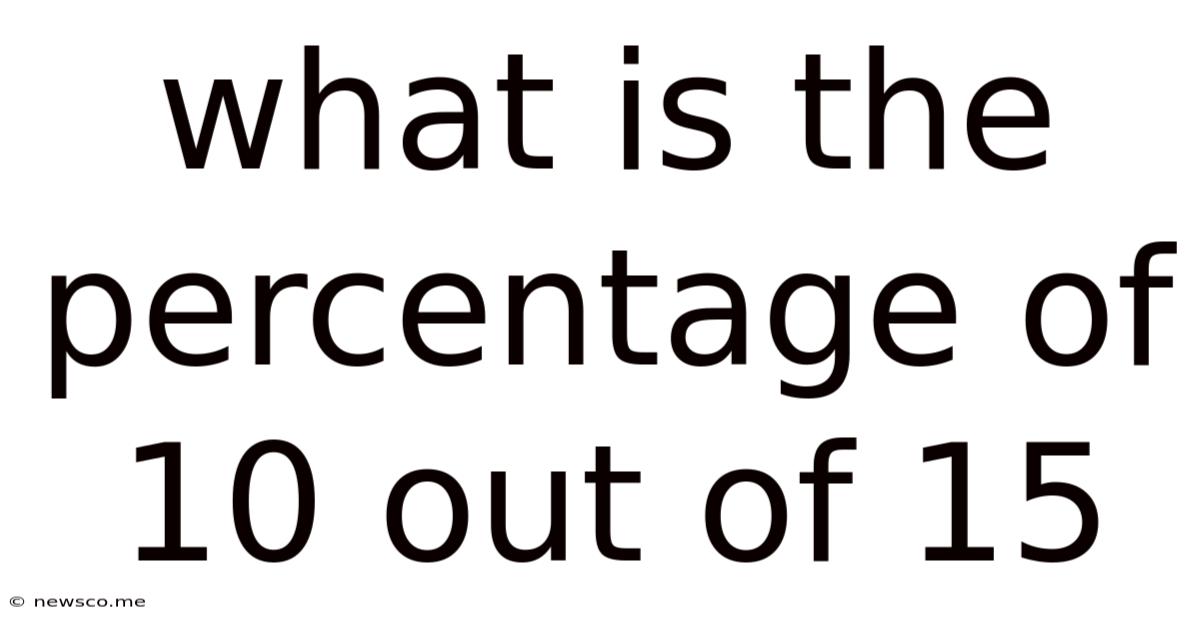
Table of Contents
What is the Percentage of 10 out of 15? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday finances to complex scientific analyses. Understanding how to determine percentages allows you to make informed decisions, interpret data effectively, and solve problems accurately. This comprehensive guide will delve into the intricacies of calculating percentages, using the example of "What is the percentage of 10 out of 15?" as a springboard to explore various methods and applications.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "percent," meaning "out of one hundred." For example, 50% represents 50 out of 100, which simplifies to one-half (1/2) or 0.5 as a decimal. Percentages are a convenient way to represent proportions, enabling easy comparisons and interpretations of data.
Calculating the Percentage of 10 out of 15: The Direct Method
The most straightforward method to calculate the percentage of 10 out of 15 involves the following steps:
-
Form a Fraction: Express the given numbers as a fraction: 10/15.
-
Convert to Decimal: Divide the numerator (10) by the denominator (15): 10 ÷ 15 = 0.666... (This is a recurring decimal).
-
Multiply by 100: Multiply the decimal result by 100 to convert it into a percentage: 0.666... × 100 = 66.666...%
-
Round (if necessary): Round the percentage to the desired level of precision. Rounding to two decimal places, we get 66.67%.
Therefore, 10 out of 15 represents 66.67%.
Alternative Methods: Proportions and Cross-Multiplication
While the direct method is efficient, understanding alternative approaches enhances your problem-solving capabilities. The method of proportions utilizes the concept of equivalent ratios to solve percentage problems.
We can set up a proportion:
- x/100 = 10/15
Where 'x' represents the unknown percentage. Cross-multiplying gives:
- 15x = 1000
Solving for 'x':
- x = 1000/15 = 66.67%
This method provides an alternative pathway to the same solution.
Practical Applications: Real-World Examples
Understanding percentage calculations has immense practical value across various domains:
1. Finance and Budgeting:
- Calculating interest rates: Banks and financial institutions use percentages extensively to determine interest earned on savings accounts or interest payable on loans. Understanding percentage calculations helps you manage your finances effectively.
- Analyzing discounts and sales: Retailers commonly advertise discounts as percentages. Knowing how to calculate percentages enables you to determine the actual price reduction and make informed purchasing decisions. For instance, a 20% discount on a $100 item equates to a $20 reduction, resulting in a final price of $80.
- Tax calculations: Governments levy taxes on income, sales, and goods and services, often expressed as percentages. Calculating these taxes accurately is crucial for financial planning and compliance.
2. Academic Performance:
- Grading systems: Many educational institutions use percentages to represent grades, providing a clear indication of student performance relative to the total marks attainable.
- Test scores: Percentage scores on examinations provide a standardized measure of performance, allowing for comparison across different tests and individuals.
3. Scientific and Statistical Analysis:
- Data representation: Percentages are frequently employed in representing data in graphs, charts, and tables, simplifying the interpretation of complex datasets.
- Probability calculations: Percentages are invaluable in probability theory, enabling the expression of the likelihood of events occurring. For instance, a 75% probability of rain implies a 75 out of 100 chance of precipitation.
4. Everyday Life:
- Tip calculations: Calculating tips in restaurants or other service establishments involves determining a percentage of the total bill.
- Ingredient proportions: Cooking recipes often use percentages to specify ingredient ratios. For example, a recipe might call for 60% flour and 40% water.
Beyond the Basics: Advanced Percentage Calculations
While calculating the percentage of 10 out of 15 provides a foundational understanding, let's explore more complex scenarios:
1. Percentage Increase and Decrease:
Calculating percentage increases or decreases requires understanding the initial and final values. The formula for percentage increase is:
[(Final Value - Initial Value) / Initial Value] × 100%
Similarly, the formula for percentage decrease is:
[(Initial Value - Final Value) / Initial Value] × 100%
For example, if the price of an item increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] × 100% = 20%
2. Percentage Change:
This encompasses both increases and decreases and is particularly useful when comparing values over time.
The formula for percentage change is:
[(New Value - Old Value) / Old Value] × 100%
A positive result indicates an increase, while a negative result indicates a decrease.
3. Finding the Original Value:
Sometimes, you might know the percentage and the final value after a percentage increase or decrease, and you need to determine the original value. This involves reverse percentage calculations.
Let's say an item is discounted by 25% and costs $75 after the discount. To find the original price (x):
- x - 0.25x = $75
- 0.75x = $75
- x = $75 / 0.75 = $100
Therefore, the original price was $100.
Mastering Percentages: Tips and Tricks
- Practice regularly: The more you practice percentage calculations, the more proficient you will become.
- Use a calculator: For complex calculations, utilizing a calculator ensures accuracy.
- Understand the concepts: Focusing on the underlying principles enhances your problem-solving abilities.
- Break down complex problems: Divide complex percentage problems into smaller, manageable steps.
- Check your answers: Always verify your results to ensure accuracy.
Conclusion: The Ubiquity of Percentages
This comprehensive guide has illustrated the importance of percentage calculations and provided various methods to determine percentages, using the example of "What is the percentage of 10 out of 15?" as a starting point. Understanding and mastering percentages is essential for success in various aspects of life, from personal finance and academics to scientific research and daily decision-making. By practicing and applying these methods, you will gain confidence and proficiency in handling percentage-related problems. Remember, consistent practice is key to mastering this crucial mathematical skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 10 Out Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.