What Is The Prime Factorization For 110
News Co
Apr 06, 2025 · 5 min read
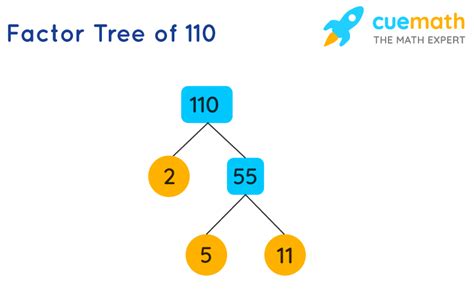
Table of Contents
What is the Prime Factorization for 110? A Deep Dive into Prime Numbers and Factorization
Prime factorization – it sounds complicated, but it's a fundamental concept in mathematics with surprisingly broad applications. Understanding prime factorization is key to grasping a range of mathematical ideas, from simplifying fractions to tackling complex cryptographic systems. This article will thoroughly explore the concept of prime factorization, using the number 110 as our illustrative example. We'll go beyond simply finding the answer and delve into the underlying principles, offering explanations suitable for both beginners and those seeking a deeper understanding.
What is Prime Factorization?
Prime factorization is the process of finding the prime numbers that, when multiplied together, equal a given number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Numbers that are not prime are called composite numbers.
The prime factorization of a number is unique; that is, there's only one set of prime numbers that will multiply to give that specific number (ignoring the order of the factors). This uniqueness is a cornerstone of number theory.
Finding the Prime Factorization of 110
Let's find the prime factorization of 110. We can use a method called the factor tree.
Step-by-Step Factor Tree Method
-
Start with the number: Begin with 110 at the top of your tree.
-
Find a pair of factors: Find any two numbers that multiply to 110. A good starting point is often the smallest prime number, 2. Since 110 is an even number, it's divisible by 2. 110 = 2 x 55. We write 2 and 55 as branches extending from 110.
-
Continue factoring: Now, examine each branch. 2 is a prime number, so we circle it. 55 is composite. We need to find its factors. 55 = 5 x 11. We add branches from 55 to 5 and 11.
-
Identify prime factors: Both 5 and 11 are prime numbers, so we circle them.
-
Write the prime factorization: We've reached the end of our branches, and all the numbers are prime. The prime factorization of 110 is 2 x 5 x 11.
Here's a visual representation of the factor tree:
110
/ \
2 55
/ \
5 11
Therefore, the prime factorization of 110 is 2 x 5 x 11.
Beyond the Factor Tree: Alternative Methods
While the factor tree is a visually intuitive method, especially for beginners, there are other approaches to finding the prime factorization of a number.
Repeated Division
This method involves repeatedly dividing the number by the smallest prime number that divides it evenly until you reach 1.
-
Start with 110: Divide 110 by 2 (the smallest prime number): 110 ÷ 2 = 55.
-
Continue dividing: Now, divide 55 by the smallest prime number that divides it evenly, which is 5: 55 ÷ 5 = 11.
-
Final prime: 11 is a prime number. We have reached 1 after repeated division.
The prime factors are the divisors used in the process: 2, 5, and 11. Thus, the prime factorization is 2 x 5 x 11.
The Uniqueness of Prime Factorization: The Fundamental Theorem of Arithmetic
The fact that every composite number can be expressed as a unique product of primes (disregarding the order) is known as the Fundamental Theorem of Arithmetic. This theorem is fundamental to many areas of number theory and algebra. It's not just a convenient method; it's a foundational truth about the structure of whole numbers.
Applications of Prime Factorization
The concept of prime factorization might seem abstract, but it has numerous practical applications:
-
Simplifying fractions: To simplify a fraction to its lowest terms, you find the prime factorization of both the numerator and the denominator. Then, you cancel out common prime factors.
-
Finding the greatest common divisor (GCD) and least common multiple (LCM): Prime factorization is the most efficient way to calculate the GCD and LCM of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder, while the LCM is the smallest number that is a multiple of all the given numbers.
-
Cryptography: Prime factorization plays a crucial role in modern cryptography, particularly in systems like RSA encryption. The security of these systems relies on the difficulty of factoring very large numbers into their prime components. Breaking these codes would require incredibly powerful computers and sophisticated algorithms.
-
Abstract Algebra: Prime factorization extends beyond elementary arithmetic and forms the basis for understanding algebraic structures like rings and fields.
-
Number Theory Research: Prime factorization continues to be a subject of ongoing mathematical research, with unsolved problems such as efficiently factoring large numbers remaining a significant challenge.
Advanced Topics: Exploring Beyond the Basics
For those seeking a deeper dive, several more advanced concepts build upon the foundation of prime factorization:
-
Sieve of Eratosthenes: This ancient algorithm provides an efficient method for finding all prime numbers up to a specified integer.
-
Prime Number Theorem: This theorem provides an approximation for the number of primes less than a given integer, offering insights into the distribution of prime numbers.
-
Mersenne Primes: These are prime numbers that are one less than a power of two (e.g., 7 = 2³ - 1, 31 = 2⁵ - 1). The search for Mersenne primes is a continuing area of research, often involving distributed computing projects.
-
Twin Primes: These are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13). The existence of infinitely many twin primes remains a significant unsolved problem in number theory.
Conclusion: The Enduring Importance of Prime Factorization
The seemingly simple concept of prime factorization underpins a vast amount of mathematical theory and practical applications. From simplifying fractions to securing online transactions, the ability to break down composite numbers into their prime components proves to be surprisingly powerful and versatile. By understanding prime factorization, we gain a deeper appreciation for the fundamental structure of numbers and the elegance of mathematics itself. Whether you're a student grappling with elementary arithmetic or a researcher pushing the boundaries of number theory, mastering prime factorization is an essential step on the journey. The seemingly simple example of 110 – 2 x 5 x 11 – represents a fundamental building block in this exciting mathematical world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization For 110 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.