What Is The Prime Factorization Of 260
News Co
Apr 03, 2025 · 6 min read
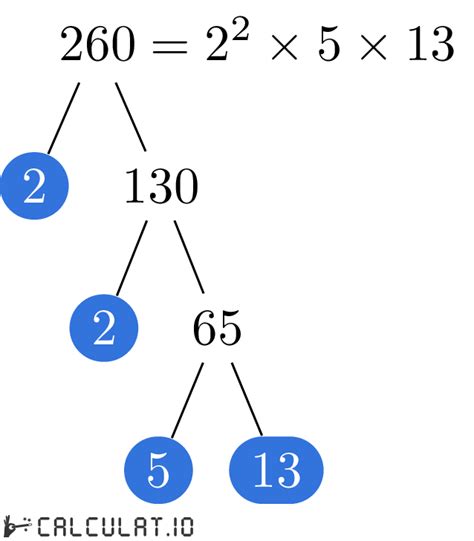
Table of Contents
What is the Prime Factorization of 260? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What is the prime factorization of 260?" opens a door to a fascinating world of number theory, exploring fundamental concepts crucial to mathematics and computer science. This article delves into the process of finding the prime factorization of 260, explaining the underlying principles, and demonstrating its application in various mathematical contexts. We'll go beyond just providing the answer, exploring the broader implications of prime factorization.
Understanding Prime Numbers and Prime Factorization
Before tackling the prime factorization of 260, let's establish a firm grasp of the key concepts:
Prime Numbers: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This means it's only divisible without a remainder by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Note that 1 is not considered a prime number.
Prime Factorization: Prime factorization (also called prime decomposition) is the process of finding which prime numbers multiply together to make the original number. Every composite number (a number greater than 1 that is not prime) can be expressed uniquely as a product of prime numbers. This is known as the Fundamental Theorem of Arithmetic. This unique representation is crucial in various mathematical operations.
Finding the Prime Factorization of 260: A Step-by-Step Approach
Now, let's find the prime factorization of 260. We'll employ a method called the "factor tree."
-
Start with the original number: We begin with 260.
-
Find the smallest prime factor: The smallest prime number is 2. Since 260 is an even number, it's divisible by 2. We divide 260 by 2: 260 ÷ 2 = 130.
-
Continue factoring: Now we have 130. Again, 130 is an even number, divisible by 2: 130 ÷ 2 = 65.
-
Moving to larger primes: 65 is no longer divisible by 2. Let's try the next prime number, 3. 65 is not divisible by 3 (6 + 5 = 11, which is not divisible by 3).
-
Finding the next prime factor: The next prime is 5. 65 is divisible by 5: 65 ÷ 5 = 13.
-
Reaching a prime number: We've reached 13, which is a prime number. We can't factor it further.
Therefore, the prime factorization of 260 is 2 x 2 x 5 x 13, which can also be written as 2² x 5 x 13.
Visualizing the Prime Factorization with a Factor Tree
A factor tree visually represents this process:
260
/ \
2 130
/ \
2 65
/ \
5 13
This tree clearly shows the prime factors branching down from the original number until we reach only prime numbers at the bottom.
Applications of Prime Factorization
Prime factorization isn't just an abstract mathematical concept; it has significant practical applications in several fields:
1. Cryptography
Prime numbers are fundamental to modern cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring very large numbers into their prime components. The larger the prime numbers used, the more secure the encryption.
2. Number Theory
Prime factorization is a cornerstone of number theory, used to prove various theorems and solve complex problems related to integers. Understanding prime factorization provides insights into the structure and properties of numbers.
3. Computer Science
Algorithms for finding prime factorizations are crucial in computer science for tasks like cryptography, data compression, and random number generation. The efficiency of these algorithms is a subject of ongoing research.
4. Simplifying Fractions
In arithmetic, prime factorization is extremely useful for simplifying fractions. By finding the prime factors of the numerator and denominator, we can easily identify common factors to cancel, leading to a simplified fraction in its lowest terms.
For example, consider the fraction 260/520. We know from our prime factorization that 260 = 2² x 5 x 13 and we can find the prime factorization of 520 as 2³ x 5 x 13. Therefore:
260/520 = (2² x 5 x 13) / (2³ x 5 x 13) = 1/2
5. Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Prime factorization is also a powerful tool for finding the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers. The GCD is the largest number that divides all the numbers without leaving a remainder. The LCM is the smallest number that is a multiple of all the numbers.
Let's find the GCD and LCM of 260 and another number, say 180 (whose prime factorization is 2² x 3² x 5).
-
GCD: To find the GCD, we identify the common prime factors raised to the lowest power present in both factorizations. Both 260 (2² x 5 x 13) and 180 (2² x 3² x 5) contain 2² and 5. Thus, GCD(260, 180) = 2² x 5 = 20.
-
LCM: To find the LCM, we take all prime factors from both factorizations, raised to the highest power present. The prime factors are 2, 3, 5, and 13. The highest powers are 2², 3², 5, and 13. Thus, LCM(260, 180) = 2² x 3² x 5 x 13 = 2340.
Beyond the Basics: Advanced Concepts Related to Prime Factorization
The concept of prime factorization extends to more advanced areas of mathematics, including:
-
Modular Arithmetic: Prime factorization plays a crucial role in modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value (the modulus). This is fundamental to cryptography.
-
Number-Theoretic Functions: Several number-theoretic functions, such as Euler's totient function, rely heavily on prime factorization. These functions provide valuable information about the properties of integers.
-
Algebraic Number Theory: The concept extends to algebraic number fields, where prime factorization can become more complex, involving prime ideals instead of just prime numbers.
-
The Riemann Hypothesis: This unsolved Millennium Prize Problem in mathematics deeply relates to the distribution of prime numbers and their properties, showcasing the ongoing importance of prime factorization in mathematical research.
Conclusion: The Significance of Prime Factorization
The seemingly straightforward prime factorization of 260 – 2² x 5 x 13 – reveals a profound connection to fundamental mathematical concepts. This simple process underlies many advanced mathematical and computational techniques used across diverse fields, from secure online transactions to solving complex number-theoretic problems. Understanding prime factorization is not merely about finding the factors of a number; it is about understanding the building blocks of arithmetic and their profound implications across various branches of mathematics and computer science. The journey from a simple number to its prime factors unlocks a world of mathematical possibilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 260 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.