What Is The Prime Factorization Of 65
News Co
Apr 06, 2025 · 5 min read
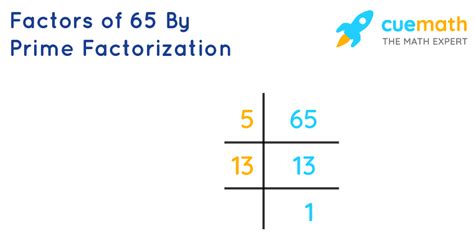
Table of Contents
What is the Prime Factorization of 65? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What is the prime factorization of 65?" opens a door to a fascinating world of number theory. While the answer itself is straightforward, exploring the process and the underlying concepts reveals fundamental principles crucial to various areas of mathematics and computer science. This article will not only answer the question but also delve into the concepts of prime numbers, factorization, and their significance.
Understanding Prime Numbers
Before tackling the prime factorization of 65, let's define the key player: the prime number. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 2 is the only even prime number; all other even numbers are divisible by 2.
The fundamental theorem of arithmetic states that every integer greater than 1 is either a prime number itself or can be represented as a unique product of prime numbers. This uniqueness is a cornerstone of number theory. This theorem guarantees that there's only one way to express a number as a product of primes (ignoring the order of the factors).
Methods for Finding Prime Factors
Several methods exist to find the prime factors of a number. Let's explore a few, illustrating them with the number 65:
1. Trial Division
This is the most straightforward method, especially for smaller numbers. We systematically divide the number by prime numbers, starting with the smallest.
- Divide by 2: 65 is not divisible by 2 (it's odd).
- Divide by 3: 65 is not divisible by 3 (6 + 5 = 11, which is not divisible by 3).
- Divide by 5: 65 is divisible by 5 (65 ÷ 5 = 13).
We've found one prime factor: 5. The result of the division, 13, is also a prime number. Therefore, the prime factorization of 65 is 5 x 13.
2. Factor Tree
A factor tree is a visual representation of the factorization process. We start with the number and branch out, breaking it down into its factors until all branches end in prime numbers.
65
/ \
5 13
This clearly shows that the prime factorization of 65 is 5 x 13.
3. Using the Sieve of Eratosthenes (for a range of numbers)
While not directly used for finding the prime factors of a single number, the Sieve of Eratosthenes is a powerful algorithm to find all prime numbers up to a specified integer. It's a useful tool when dealing with a range of numbers or when you need to identify prime factors within a larger context.
The Sieve operates by iteratively marking as composite (non-prime) the multiples of each prime, starting with 2. The numbers that remain unmarked are prime. While this is less efficient for a single number like 65, it's invaluable for generating a list of primes within a given range.
The Prime Factorization of 65: 5 x 13
Based on the methods described above, we conclusively find that the prime factorization of 65 is 5 x 13. Both 5 and 13 are prime numbers, and their product is 65. This factorization is unique, as guaranteed by the fundamental theorem of arithmetic.
Applications of Prime Factorization
The seemingly simple act of finding prime factors has far-reaching applications in various fields:
1. Cryptography
Prime numbers are at the heart of modern cryptography. Many encryption algorithms, such as RSA (Rivest-Shamir-Adleman), rely on the difficulty of factoring very large numbers into their prime components. The security of these systems hinges on the computational infeasibility of factoring such enormous numbers, making them essential for secure online transactions and data protection.
2. Number Theory and Mathematics
Prime factorization is fundamental to many branches of number theory. Concepts like modular arithmetic, congruences, and the distribution of prime numbers are heavily reliant on the properties of prime numbers and their factorizations. This field continues to be a source of ongoing mathematical research.
3. Computer Science and Algorithms
Prime factorization is used in algorithms related to data structures, cryptography, and random number generation. Efficient algorithms for prime factorization are crucial for ensuring the security of cryptographic systems and improving computational efficiency in various applications.
Beyond 65: Exploring Larger Numbers
While the prime factorization of 65 is relatively simple, finding the prime factors of larger numbers can become computationally intensive. For very large numbers, specialized algorithms are needed, and even powerful computers can struggle to factor them within a reasonable time frame. This computational difficulty is what makes prime factorization crucial for the security of modern cryptographic systems.
Conclusion: The Importance of Understanding Prime Factorization
This in-depth exploration of the prime factorization of 65 has highlighted not only the process itself but also the significance of prime numbers and factorization in various fields. From the simple act of breaking down a number into its prime components to the complex algorithms used in cryptography, the concept of prime factorization reveals fundamental mathematical principles with far-reaching implications. Understanding this seemingly simple concept opens a world of deeper mathematical understanding and its application in modern technologies. The prime factorization of 65, while seemingly trivial, acts as a perfect entry point into this fascinating realm.
Latest Posts
Latest Posts
-
How Long Is 100cm In Inches
Apr 07, 2025
-
What Is 3 Months In Weeks
Apr 07, 2025
-
1 3 Plus 1 3 As A Fraction
Apr 07, 2025
-
What Is The Square Root Of 189
Apr 07, 2025
-
How To Find The Area Of The Shaded Sector
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
