What Is The Prime Factorization Of 700
News Co
Apr 03, 2025 · 5 min read
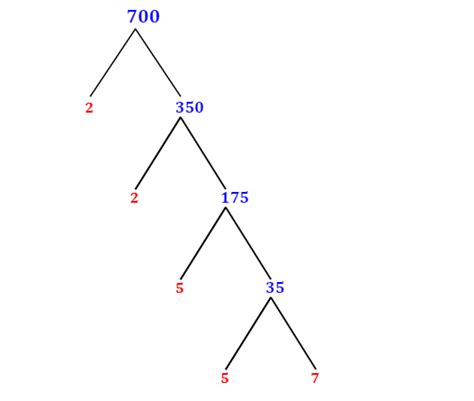
Table of Contents
What is the Prime Factorization of 700? A Deep Dive into Prime Numbers and Factorization
Prime factorization, a cornerstone of number theory, is the process of breaking down a composite number into its prime number components. Understanding this process is crucial in various mathematical fields, from cryptography to simplifying complex expressions. This article will explore the prime factorization of 700, explaining the method, the significance of prime numbers, and providing further examples to solidify your understanding.
Understanding Prime Numbers and Prime Factorization
Before delving into the prime factorization of 700, let's establish a firm understanding of the fundamental concepts.
What are Prime Numbers?
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, it's only divisible by 1 and itself without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number.
What is Prime Factorization?
Prime factorization, also known as prime decomposition, is the process of expressing a composite number (a number that is not prime) as a product of its prime factors. This representation is unique for every composite number, meaning there's only one way to express it as a product of primes (ignoring the order of the factors).
Finding the Prime Factorization of 700
Now, let's tackle the prime factorization of 700. We'll use a method called the factor tree.
-
Start with the number 700.
-
Find the smallest prime number that divides 700. This is 2. Divide 700 by 2: 700 / 2 = 350.
-
Repeat the process with 350. Again, the smallest prime divisor is 2: 350 / 2 = 175.
-
Continue with 175. Now, 2 doesn't divide 175 evenly. The next prime number is 3, but 3 doesn't divide 175 either. The next prime is 5, and 175 is divisible by 5: 175 / 5 = 35.
-
Proceed with 35. Again, 5 divides 35: 35 / 5 = 7.
-
The final result is 7, which is a prime number.
We can visually represent this process using a factor tree:
700
/ \
2 350
/ \
2 175
/ \
5 35
/ \
5 7
Therefore, the prime factorization of 700 is 2 x 2 x 5 x 5 x 7, which can also be written as 2² x 5² x 7.
Significance of Prime Factorization
Prime factorization isn't just an academic exercise; it has significant applications in various fields:
-
Cryptography: Many encryption methods rely on the difficulty of factoring large numbers into their prime components. The security of RSA encryption, for instance, depends on this computational challenge. Factoring large numbers with hundreds of digits is computationally intensive, making it a strong foundation for secure communication.
-
Simplifying Fractions: Prime factorization is crucial in simplifying fractions. By finding the prime factors of the numerator and denominator, you can easily identify common factors and cancel them out to obtain the simplest form of the fraction.
-
Solving Algebraic Equations: Prime factorization plays a role in solving certain types of algebraic equations, particularly those involving quadratic or higher-order polynomials. Factoring the polynomial allows you to find the roots (solutions) of the equation more efficiently.
-
Number Theory: Prime factorization is a fundamental concept in number theory, which deals with the properties of integers. It underlies many theorems and proofs in this field.
-
Modular Arithmetic: Prime factorization is crucial in modular arithmetic, which involves performing arithmetic operations within a specific range (modulo). Many cryptographic protocols leverage the properties of prime numbers and modular arithmetic for secure data transmission.
Alternative Methods for Prime Factorization
While the factor tree method is intuitive and visually appealing, other methods can also be used to find the prime factorization of a number.
Repeated Division Method
This method involves repeatedly dividing the number by the smallest prime number that divides it until you reach 1.
For 700:
- 700 / 2 = 350
- 350 / 2 = 175
- 175 / 5 = 35
- 35 / 5 = 7
- 7 / 7 = 1
The prime factors are 2, 2, 5, 5, and 7.
Using a Prime Factorization Calculator (for larger numbers)
For very large numbers, using a prime factorization calculator can be significantly faster and more efficient than manual methods. These calculators utilize advanced algorithms optimized for prime factorization.
Practice Problems
Let's test your understanding with some practice problems:
-
Find the prime factorization of 360: Try using both the factor tree and repeated division methods. You should get 2³ x 3² x 5.
-
Find the prime factorization of 1008: This is a slightly larger number, so the factor tree might be more manageable. The answer is 2⁴ x 3² x 7.
-
Find the greatest common divisor (GCD) of 700 and 360 using their prime factorizations: Remember that the GCD is the product of the common prime factors raised to the lowest power. In this case, the GCD(700, 360) = 2² x 5 = 20.
-
Find the least common multiple (LCM) of 700 and 360 using their prime factorizations: The LCM is the product of all prime factors raised to the highest power. The LCM(700, 360) = 2³ x 3² x 5² x 7 = 12600
Conclusion
Understanding prime factorization is fundamental to numerous mathematical concepts and applications. The prime factorization of 700, 2² x 5² x 7, serves as a clear example of how to decompose a composite number into its prime components using various methods. Mastering this skill opens doors to deeper understanding in number theory, algebra, and cryptography. Remember to practice with different numbers to solidify your understanding and explore the fascinating world of prime numbers.
Latest Posts
Latest Posts
-
How To Make An Improper Fraction Into A Proper Fraction
Apr 04, 2025
-
What Is 5 To The 4th Power
Apr 04, 2025
-
What Is The Square Root Of 71
Apr 04, 2025
-
Inverse Matrix Calculator Step By Step
Apr 04, 2025
-
What Are The Factors Of 95
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 700 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
