What Is The Prime Factorization Of 735
News Co
Apr 02, 2025 · 5 min read
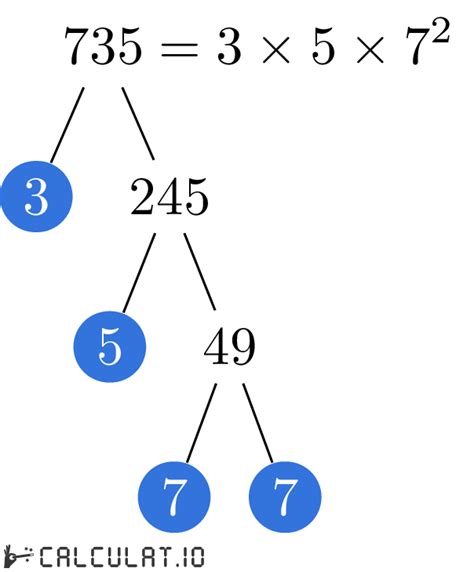
Table of Contents
What is the Prime Factorization of 735? A Deep Dive into Prime Numbers and Factorization
Prime factorization – a seemingly simple concept in mathematics, yet it forms the bedrock of numerous advanced mathematical principles and cryptographic applications. Understanding prime factorization is crucial not only for academic pursuits but also for grasping the security behind online transactions and data encryption. This article will explore the prime factorization of 735 in detail, explaining the process, the significance of prime numbers, and offering some related applications.
Understanding Prime Numbers
Before diving into the factorization of 735, let's solidify our understanding of prime numbers. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In simpler terms, it's only divisible by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. These numbers are the building blocks of all other natural numbers, a fundamental concept in number theory.
Conversely, a composite number is a positive integer that has at least one divisor other than 1 and itself. For instance, 6 is a composite number because it's divisible by 2 and 3. 1 is neither prime nor composite.
The Importance of Prime Numbers
Prime numbers hold a unique position in mathematics and have profound implications in various fields:
-
Cryptography: The security of many encryption algorithms, including RSA (widely used for secure online transactions), relies on the difficulty of factoring large composite numbers into their prime factors. Finding the prime factors of a very large number is computationally intensive, making these encryption methods secure.
-
Number Theory: Prime numbers are central to many theorems and conjectures in number theory, such as the Riemann Hypothesis, one of the most significant unsolved problems in mathematics.
-
Computer Science: Prime numbers are utilized in hash functions, which are crucial for data structures and algorithms used in computer science.
Finding the Prime Factorization of 735
Now, let's determine the prime factorization of 735. We'll use a method called prime factorization by division. This method involves repeatedly dividing the number by the smallest prime number that divides it evenly until we reach 1.
Step 1: Divide by the smallest prime number.
The smallest prime number is 2. However, 735 is an odd number, so it's not divisible by 2. The next prime number is 3. Let's check if 735 is divisible by 3. The rule for divisibility by 3 is that the sum of its digits must be divisible by 3. 7 + 3 + 5 = 15, and 15 is divisible by 3. Therefore, 735 is divisible by 3.
735 ÷ 3 = 245
Step 2: Continue dividing by prime numbers.
Now we have 245. This is not divisible by 2 or 3. Let's check for divisibility by 5 (another prime number). Any number ending in 0 or 5 is divisible by 5. Therefore, 245 is divisible by 5.
245 ÷ 5 = 49
Step 3: Identify the remaining prime factor.
We're left with 49. 49 is not divisible by 2, 3, or 5. However, 49 is a perfect square: 7 x 7 = 49. Thus, 49 is divisible by 7, which is a prime number.
49 ÷ 7 = 7
Step 4: The final prime factorization.
We have reached 7, which is a prime number. This means we've completed the factorization. Therefore, the prime factorization of 735 is 3 x 5 x 7 x 7, or 3 x 5 x 7².
Alternative Methods for Prime Factorization
While the method of repeated division is straightforward, there are other approaches to finding the prime factorization of a number. Let's briefly discuss a couple of alternatives:
1. Factor Tree: A factor tree is a visual method where you break down the number into smaller factors until you reach only prime numbers. It's often used as a teaching tool to help visualize the process. For 735, the factor tree would look something like this:
735
/ \
3 245
/ \
5 49
/ \
7 7
2. Using a Prime Factorization Calculator: Numerous online calculators can perform prime factorization instantly. These calculators are particularly useful for large numbers where manual calculation becomes tedious. However, understanding the underlying process remains essential for comprehending the mathematical principles involved.
Applications of Prime Factorization
Beyond the fundamental concepts of number theory, prime factorization has several real-world applications:
-
Cryptography, as mentioned earlier, relies heavily on the difficulty of factoring large numbers. The security of many online banking systems, secure communications, and digital signatures depend on this. Breaking these encryption systems requires finding the prime factors of very large composite numbers, a task that is computationally infeasible with current technology.
-
Coding Theory: Prime numbers play a role in error-correcting codes, which are used to detect and correct errors in data transmission. These codes are vital in various applications, including telecommunications and data storage.
-
Computer Graphics: Some algorithms used in computer graphics employ prime numbers for efficient computations and rendering.
-
Hashing Algorithms: In computing, hashing algorithms use prime numbers to ensure a more even distribution of hashed values, contributing to the efficiency and effectiveness of data structures like hash tables.
Conclusion: The Significance of Prime Factorization
The prime factorization of 735, 3 x 5 x 7², might seem like a simple mathematical exercise. However, the process of prime factorization and the properties of prime numbers are fundamental to many advanced mathematical concepts and have crucial applications in diverse fields, especially in the realm of cryptography and computer science. Understanding prime factorization is not merely an academic pursuit; it's a key component of understanding the technology that secures our digital world. Mastering this concept provides a solid foundation for exploring more advanced areas of mathematics and its real-world applications. By applying the methods outlined above, you can confidently tackle the prime factorization of various numbers, building your mathematical skills and appreciating the profound significance of prime numbers in the fabric of mathematics and beyond.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 735 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.