What Is The Prime Factorization Of 77
News Co
Apr 03, 2025 · 6 min read
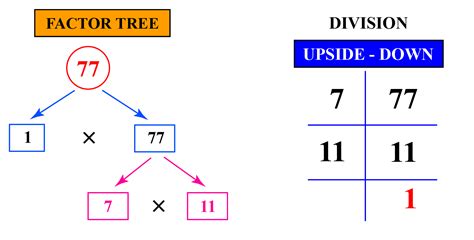
Table of Contents
What is the Prime Factorization of 77? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What is the prime factorization of 77?" opens a door to a fascinating world of number theory, prime numbers, and the fundamental building blocks of mathematics. While the answer itself is straightforward, exploring the concepts behind it unveils deeper mathematical principles and techniques useful far beyond this single calculation. This article will not only provide the answer but will also delve into the theoretical underpinnings of prime factorization, its applications, and related concepts.
Understanding Prime Numbers
Before tackling the prime factorization of 77, let's define the key player: the prime number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it cannot be expressed as a product of two smaller whole numbers. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The sequence of prime numbers is infinite, a fact proven by Euclid centuries ago. This infinity ensures that there's always a new prime number to discover, driving ongoing research in number theory. The distribution of prime numbers is also a rich area of study, with mathematicians exploring patterns and irregularities in their occurrence.
Distinguishing Prime Numbers from Composite Numbers
It's crucial to differentiate prime numbers from composite numbers. A composite number is a whole number greater than 1 that can be factored into smaller whole numbers other than 1 and itself. For example, 6 is a composite number because it can be factored as 2 x 3. The number 1 is neither prime nor composite; it's a special case in number theory. Understanding this distinction is fundamental to grasping prime factorization.
The Fundamental Theorem of Arithmetic
The foundation of prime factorization rests on the Fundamental Theorem of Arithmetic, also known as the Unique Factorization Theorem. This theorem states that every integer greater than 1 can be represented as a unique product of prime numbers, ignoring the order of the factors. This uniqueness is crucial; it means there's only one way to express a number as a product of primes. This seemingly simple statement has profound implications in various areas of mathematics and computer science.
The Uniqueness of Prime Factorization
The uniqueness of prime factorization is a powerful tool. It allows us to compare and contrast numbers based on their prime factorizations. This is particularly useful in solving problems related to greatest common divisors (GCD) and least common multiples (LCM). Understanding this uniqueness assures us that our prime factorization is correct and there's no other valid representation for the number in question.
Finding the Prime Factorization of 77
Now, let's finally tackle the prime factorization of 77. We need to find the prime numbers that multiply together to equal 77. We can approach this systematically using a method called the factor tree.
-
Start with the number 77. Since 77 is an odd number, we know it's not divisible by 2.
-
Check for divisibility by the next prime number, 3. 77 is not divisible by 3 (7 + 7 = 14, which is not divisible by 3).
-
Check for divisibility by 5. 77 does not end in 0 or 5, so it's not divisible by 5.
-
Check for divisibility by 7. 77 divided by 7 equals 11. Both 7 and 11 are prime numbers.
Therefore, the prime factorization of 77 is 7 x 11. This confirms the Fundamental Theorem of Arithmetic: 77 can be uniquely expressed as the product of the prime numbers 7 and 11.
Alternative Methods for Prime Factorization
While the factor tree is a visually intuitive method, other techniques exist for finding prime factorizations, particularly useful for larger numbers.
-
Division by Primes: This method involves systematically dividing the number by the prime numbers, starting with the smallest (2). Continue dividing by primes until the quotient becomes 1. The prime factors will be the divisors used.
-
Sieve of Eratosthenes: This method is useful for finding all prime numbers up to a certain limit. It's not directly used to find the prime factorization of a specific number, but it provides a list of primes that can then be used in the division-by-primes method.
Applications of Prime Factorization
The seemingly simple process of prime factorization has surprisingly broad applications:
-
Cryptography: Prime numbers play a crucial role in modern cryptography, forming the basis of many encryption algorithms. RSA encryption, for instance, relies on the difficulty of factoring very large numbers into their prime components.
-
Number Theory: Prime factorization is fundamental to numerous branches of number theory, including the study of modular arithmetic, Diophantine equations, and the Riemann Hypothesis.
-
Computer Science: Algorithms related to prime factorization are used in various areas of computer science, such as data compression and coding theory.
-
Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Prime factorization simplifies the calculation of the GCD and LCM of two or more numbers. This is essential in various mathematical applications and problem-solving.
Beyond 77: Exploring Larger Numbers
While the prime factorization of 77 is relatively straightforward, factoring larger numbers can be significantly more challenging. The difficulty of factoring large numbers is the cornerstone of the security of many modern cryptographic systems. As numbers grow larger, the computational effort required to find their prime factorization increases exponentially. This is why very large prime numbers are essential for secure communication and data protection.
The Difficulty of Factoring Large Numbers
The computational complexity of factoring large numbers is a subject of ongoing research in both mathematics and computer science. The development of faster factoring algorithms is a constant pursuit, while the security of cryptographic systems depends on the continued difficulty of this task. The use of very large prime numbers in these systems helps maintain the necessary level of security.
Conclusion: The Significance of Prime Factorization
The seemingly simple prime factorization of 77—7 x 11—underpins significant mathematical concepts and has far-reaching applications. The exploration of prime numbers and the Fundamental Theorem of Arithmetic unveils a world of complexity and intrigue, demonstrating the foundational role of these seemingly simple concepts in various fields. The ease of factoring 77 contrasts sharply with the difficulty of factoring vastly larger numbers, highlighting the importance of prime factorization in securing our digital world. This exploration showcases how a basic mathematical concept can have profound and unexpected implications in the broader world. From simple calculations to sophisticated cryptography, the power of prime factorization remains an enduring testament to the elegance and power of mathematics.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 12 And 8
Apr 04, 2025
-
What Percentage Is 30 Of 50
Apr 04, 2025
-
12 Weeks Is Equal To How Many Months
Apr 04, 2025
-
What Are The Factors Of 86
Apr 04, 2025
-
What Is The Factor Of 57
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 77 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
