What Is The Product 3x 5 2x 2 4x 1
News Co
May 08, 2025 · 5 min read
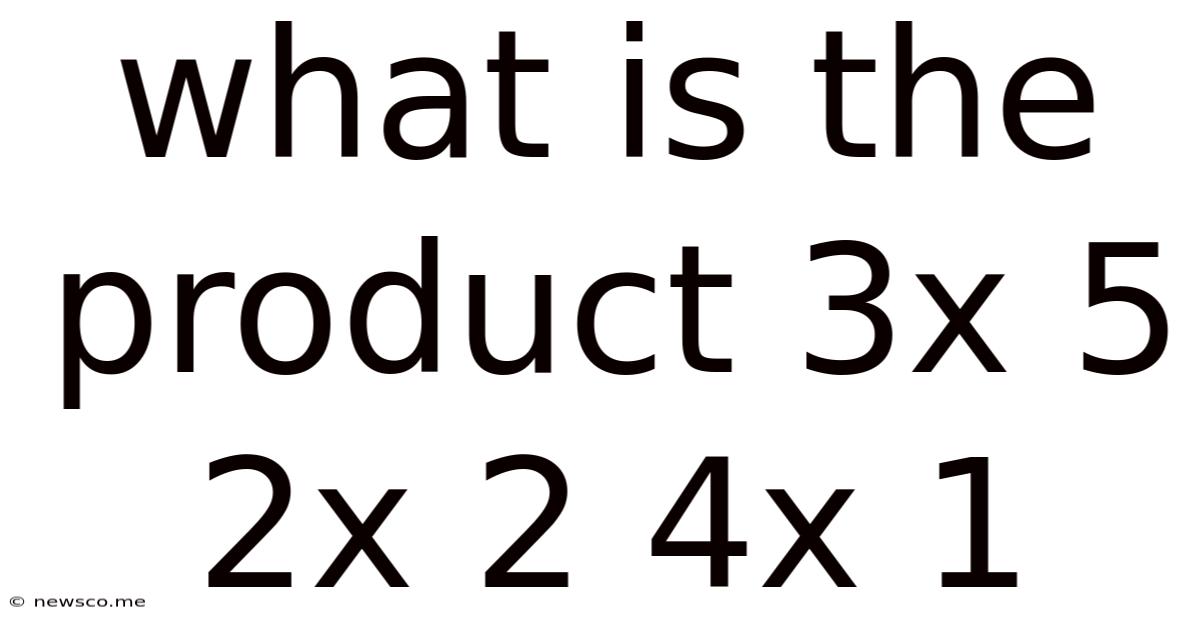
Table of Contents
What is the Product 3 x 5 x 2 x 2 x 4 x 1? A Deep Dive into Multiplication and its Applications
This seemingly simple question, "What is the product of 3 x 5 x 2 x 2 x 4 x 1?", opens the door to a fascinating exploration of multiplication, its properties, and its wide-ranging applications in various fields. While the answer itself is straightforward, understanding the underlying principles and the significance of multiplication extends far beyond a simple calculation. This article will delve into the solution, explore the concept of multiplication, discuss its properties, and showcase its relevance in diverse contexts.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is a fundamental arithmetic operation representing repeated addition. For instance, 3 x 5 can be visualized as adding three groups of five: 5 + 5 + 5 = 15. This understanding forms the basis for grasping more complex multiplication problems. Our problem, 3 x 5 x 2 x 2 x 4 x 1, can be approached systematically by breaking it down into smaller, manageable steps.
Step-by-Step Calculation:
Let's solve the equation step by step, demonstrating the process clearly:
-
3 x 5 = 15: We begin by multiplying the first two numbers.
-
15 x 2 = 30: Next, we multiply the result by the following number.
-
30 x 2 = 60: We continue the process, multiplying the current result by the next number.
-
60 x 4 = 240: The multiplication continues, building on the previous result.
-
240 x 1 = 240: Finally, multiplying by 1 doesn't change the value; the product remains 240.
Therefore, the product of 3 x 5 x 2 x 2 x 4 x 1 is 240.
The Commutative Property: Rearranging for Easier Calculation
Multiplication possesses a crucial property known as the commutative property. This property states that the order of numbers in a multiplication problem does not affect the final product. For example, 3 x 5 is the same as 5 x 3. This understanding allows us to rearrange our equation to simplify the calculation. We can group numbers together for easier mental math:
(3 x 5) x (2 x 2) x (4 x 1) = 15 x 4 x 4 = 60 x 4 = 240
This demonstrates the flexibility and efficiency gained by understanding the commutative property.
Beyond the Basics: Exploring the Properties of Multiplication
The commutative property is just one of several important properties associated with multiplication. Let's explore a few more:
-
Associative Property: This property states that the grouping of numbers in a multiplication problem doesn't alter the result. For instance, (2 x 3) x 4 = 2 x (3 x 4). This allows us to group numbers strategically for easier computation.
-
Distributive Property: This property links multiplication and addition. It states that multiplying a number by a sum is equivalent to multiplying the number by each term in the sum and then adding the results. For example, 2 x (3 + 4) = (2 x 3) + (2 x 4) = 14.
-
Identity Property: Multiplying any number by 1 results in the same number. This is evident in our problem where multiplying by 1 at the end did not change the product.
-
Zero Property: Multiplying any number by 0 always results in 0. This is a crucial property in various mathematical applications.
The Significance of Multiplication: Real-World Applications
The seemingly simple operation of multiplication plays a critical role in numerous aspects of our lives. Its applications span various fields:
1. Everyday Calculations:
From calculating the total cost of groceries to determining the area of a room, multiplication is constantly used in our daily routines. Calculating the total price of multiple items at the same cost is a direct application of multiplication.
2. Engineering and Construction:
In engineering and construction, multiplication is fundamental for calculations involving measurements, volumes, and material quantities. Estimating the amount of concrete needed for a foundation or calculating the dimensions of a building structure relies heavily on multiplication. Even simple tasks like calculating the number of bricks needed for a wall use multiplication.
3. Finance and Business:
In finance and business, multiplication is vital for calculating profits, losses, interest, and investments. Calculating compound interest, determining the total revenue from sales, or figuring out the cost of producing a certain number of units all involve multiplication.
4. Science and Technology:
Multiplication is essential in scientific and technological fields. Calculations involving speeds, distances, masses, and forces all require multiplication. In computer science, multiplication is a core operation in various algorithms and calculations.
5. Data Analysis and Statistics:
In data analysis and statistics, multiplication is used extensively in calculating averages, percentages, and probabilities. Many statistical formulas and calculations rely heavily on this fundamental operation.
Expanding the Scope: Multiplication in Advanced Mathematics
Moving beyond basic arithmetic, multiplication finds its place in advanced mathematical concepts:
-
Algebra: Multiplication is a fundamental operation in algebraic equations and expressions. Solving for unknown variables often involves manipulating equations where multiplication plays a central role.
-
Calculus: Differentiation and integration, core concepts in calculus, involve repeated multiplications and limits. Many formulas in calculus directly utilize multiplication for evaluating derivatives and integrals.
-
Linear Algebra: Matrix multiplication is a crucial operation in linear algebra, used to manipulate and solve systems of linear equations. This has applications in computer graphics, machine learning, and various engineering disciplines.
Conclusion: The Ubiquity of Multiplication
This exploration has demonstrated that the simple question, "What is the product of 3 x 5 x 2 x 2 x 4 x 1?", unveils a rich understanding of multiplication and its far-reaching implications. From basic arithmetic to advanced mathematical concepts and real-world applications, multiplication is an indispensable operation that underpins numerous aspects of our lives. Mastering its principles and properties empowers us to solve problems effectively and efficiently across diverse fields. Understanding the commutative, associative, distributive, identity, and zero properties provides a solid foundation for tackling more complex mathematical challenges and successfully applying this fundamental operation in various practical situations. The answer, 240, is just the beginning of a much broader and more significant mathematical journey.
Latest Posts
Latest Posts
-
A Drawing That Shows Information Like A Graph
May 08, 2025
-
Diagonals Of A Rectangle Are Perpendicular
May 08, 2025
-
Square Root Of 81 Rational Or Irrational
May 08, 2025
-
Fifty Five Dollars On A Check
May 08, 2025
-
What Is The Fraction Of 9
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Product 3x 5 2x 2 4x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.