What Is The Simplest Form Of 2/5
News Co
May 08, 2025 · 5 min read
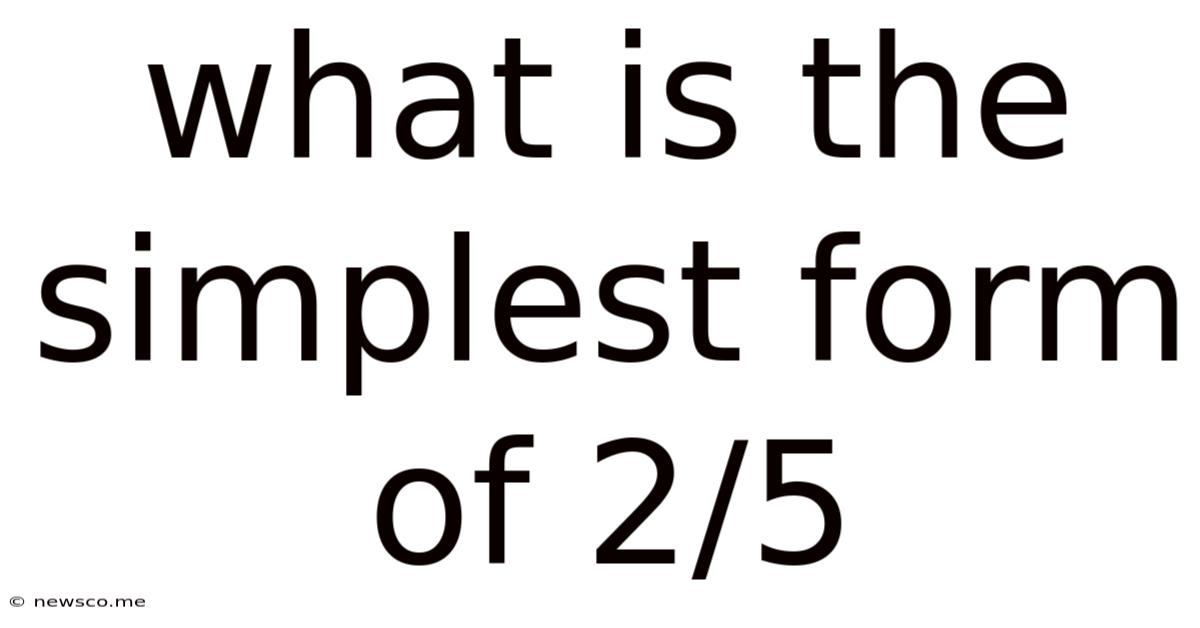
Table of Contents
What is the Simplest Form of 2/5? A Deep Dive into Fraction Simplification
The question, "What is the simplest form of 2/5?" seems deceptively simple. At first glance, the answer is obvious: 2/5. However, exploring this seemingly straightforward problem allows us to delve into the fundamental concepts of fractions, simplification, and the importance of mathematical precision. This article will not only answer the question but also provide a comprehensive understanding of fraction simplification, covering various techniques and their applications. We'll explore why 2/5 is already in its simplest form, examine the process of simplification with other fractions, and touch upon the broader implications of understanding fractions in mathematics and beyond.
Understanding Fractions: The Building Blocks
Before diving into the simplification of 2/5, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 2/5, the numerator (2) represents two parts, and the denominator (5) represents a whole divided into five equal parts.
What Does "Simplest Form" Mean?
A fraction is in its simplest form, also known as its lowest terms, when the numerator and denominator have no common factors other than 1. In other words, the greatest common divisor (GCD) of the numerator and denominator is 1. This means you cannot divide both the top and bottom numbers by any whole number greater than 1 to get smaller whole numbers.
Why 2/5 is Already in its Simplest Form
The numbers 2 and 5 are relatively prime, meaning their greatest common divisor (GCD) is 1. The only whole number that divides evenly into both 2 and 5 is 1. Therefore, 2/5 cannot be simplified further. Attempting to divide both the numerator and denominator by any other whole number would result in a fraction with a numerator or denominator that is not a whole number.
Example: Let's try dividing both 2 and 5 by 2:
2 ÷ 2 = 1 5 ÷ 2 = 2.5
The result (1/2.5) is not a fraction composed of whole numbers. This confirms that 2/5 is already in its simplest form.
Simplifying Fractions: A Step-by-Step Guide
While 2/5 is a straightforward example, let's explore the process of simplifying fractions using other examples. The core principle is to find the GCD of the numerator and denominator and divide both by it.
1. Finding the Greatest Common Divisor (GCD):
There are several methods to find the GCD, including:
- Listing Factors: List all the factors of both the numerator and denominator. The largest factor they share is the GCD.
- Prime Factorization: Express both the numerator and denominator as the product of their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
- Euclidean Algorithm: A more efficient algorithm for larger numbers, involving repeated division with remainder.
2. Dividing the Numerator and Denominator:
Once you have found the GCD, divide both the numerator and denominator by it. The resulting fraction is the simplest form.
Example 1: Simplifying 12/18
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
- GCD of 12 and 18: 6
Divide both the numerator and denominator by 6:
12 ÷ 6 = 2 18 ÷ 6 = 3
Therefore, the simplest form of 12/18 is 2/3.
Example 2: Simplifying 24/36 using Prime Factorization
- Prime factorization of 24: 2³ × 3
- Prime factorization of 36: 2² × 3²
The common prime factors are 2² and 3. Therefore, the GCD is 2² × 3 = 12.
Divide both the numerator and denominator by 12:
24 ÷ 12 = 2 36 ÷ 12 = 3
Again, the simplest form is 2/3.
Example 3: Simplifying 45/75 using the Euclidean Algorithm
Let's use the Euclidean algorithm to find the GCD of 45 and 75:
75 ÷ 45 = 1 with a remainder of 30 45 ÷ 30 = 1 with a remainder of 15 30 ÷ 15 = 2 with a remainder of 0
The last non-zero remainder is 15, which is the GCD.
Divide both the numerator and denominator by 15:
45 ÷ 15 = 3 75 ÷ 15 = 5
The simplest form is 3/5.
The Importance of Simplest Form
Expressing fractions in their simplest form is crucial for several reasons:
- Clarity and Understandability: Simpler fractions are easier to understand and visualize.
- Easier Calculations: Simplifying fractions before performing operations (addition, subtraction, multiplication, division) makes calculations significantly simpler and reduces the risk of errors.
- Consistent Representation: Ensuring fractions are in simplest form provides a standard and consistent way of representing fractional values.
Applications of Fraction Simplification
The concept of fraction simplification extends beyond basic arithmetic. It finds applications in various fields, including:
- Engineering: In designing structures or circuits, simplifying fractions ensures precise calculations and efficient resource utilization.
- Chemistry: In stoichiometry, simplifying fractions helps in determining the correct proportions of reactants and products in chemical reactions.
- Computer Science: Simplifying fractions is fundamental in algorithms and data structures dealing with rational numbers.
- Finance: In calculating proportions of investments or debts, simplified fractions provide clear and concise representation.
Conclusion: Mastering Fractions for a Stronger Foundation
While the simplest form of 2/5 is indeed 2/5, the exploration of this question has provided a deeper understanding of fraction simplification and its significance in various mathematical and practical contexts. Mastering the techniques of finding the GCD and simplifying fractions is crucial for building a strong mathematical foundation and tackling more complex problems in various fields. Remember, precision and understanding are key to success in mathematics, and simplifying fractions is a foundational step towards achieving both. The process, seemingly simple on the surface, reveals a wealth of underlying mathematical principles that empower us to tackle more complex challenges with confidence and accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Simplest Form Of 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.