What Is The Simplest Form Of 4/6
News Co
May 07, 2025 · 5 min read
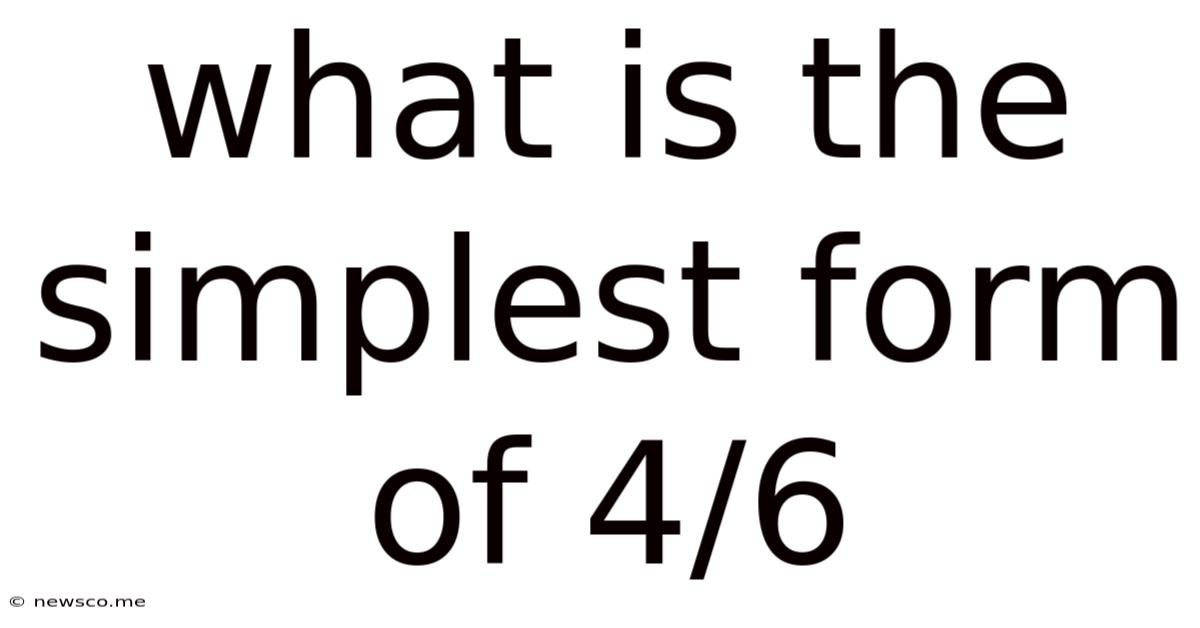
Table of Contents
What is the Simplest Form of 4/6? A Deep Dive into Fraction Simplification
The seemingly simple question, "What is the simplest form of 4/6?" opens a door to a broader understanding of fractions, their simplification, and the underlying mathematical principles. While the answer itself is straightforward, the journey to arrive at it provides valuable insights into fundamental mathematical concepts crucial for various fields, from basic arithmetic to advanced calculus. This article will not only answer the question but will also explore the process, its applications, and related concepts in detail.
Understanding Fractions: The Building Blocks
Before diving into simplification, let's establish a solid understanding of what fractions represent. A fraction, in its simplest form, represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating the number of parts we have. In the fraction 4/6, the numerator is 4.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into. In the fraction 4/6, the denominator is 6.
Therefore, 4/6 signifies that we have 4 parts out of a total of 6 equal parts.
Simplifying Fractions: The Concept of Equivalence
Simplifying a fraction means expressing it in its most concise form while maintaining its value. This is achieved by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. This process ensures we retain the same proportional relationship while reducing the complexity of the fraction.
Crucially, simplifying a fraction doesn't change its value. 4/6 is equivalent to 2/3; they represent the same proportion, just expressed differently. This concept of equivalence is fundamental to understanding fractions and their manipulations.
Finding the Simplest Form of 4/6: A Step-by-Step Guide
Let's systematically simplify 4/6 to its simplest form:
-
Identify the Numerator and Denominator: We have a numerator of 4 and a denominator of 6.
-
Find the Greatest Common Divisor (GCD): We need to find the largest number that divides both 4 and 6 evenly. The factors of 4 are 1, 2, and 4. The factors of 6 are 1, 2, 3, and 6. The largest common factor is 2.
-
Divide Both Numerator and Denominator by the GCD: We divide both the numerator (4) and the denominator (6) by the GCD (2):
4 ÷ 2 = 2 6 ÷ 2 = 3
-
The Simplest Form: The simplest form of 4/6 is therefore 2/3.
This means that 4 parts out of 6 are equivalent to 2 parts out of 3. The fraction has been reduced to its lowest terms, representing the same proportion in a more concise manner.
Beyond 4/6: Applying the Simplification Process to Other Fractions
The method used for simplifying 4/6 is applicable to any fraction. Let's look at a few examples:
- Simplifying 12/18: The GCD of 12 and 18 is 6. Dividing both by 6 gives 2/3.
- Simplifying 25/75: The GCD of 25 and 75 is 25. Dividing both by 25 gives 1/3.
- Simplifying 14/21: The GCD of 14 and 21 is 7. Dividing both by 7 gives 2/3.
Notice the recurring theme – simplifying often leads to a more manageable and easily understandable representation of the fraction.
Visualizing Fraction Simplification: A Geometric Approach
Understanding fraction simplification can be enhanced by visualizing it geometrically. Imagine a rectangular shape divided into 6 equal parts. Shading 4 of those parts represents the fraction 4/6. Now, consider grouping those 6 parts into pairs. You will have 3 groups of 2. Shading 2 of those 3 groups represents the equivalent fraction 2/3. This visual representation solidifies the concept of equivalent fractions.
Practical Applications of Fraction Simplification
Fraction simplification isn't just an abstract mathematical exercise; it has numerous practical applications:
-
Cooking and Baking: Recipes often use fractions. Simplifying fractions helps in measuring ingredients accurately and efficiently. For example, instead of using 4/6 of a cup of sugar, you can easily use 2/3.
-
Construction and Engineering: Precise measurements are vital. Simplifying fractions ensures accurate calculations and reduces potential errors.
-
Data Analysis: In data analysis and statistics, simplifying fractions helps to present data concisely and clearly.
-
Financial Calculations: Many financial calculations involve fractions and percentages. Simplification makes the calculations easier and more understandable.
-
Everyday Life: Numerous everyday situations involve sharing things proportionally, where understanding fractions and their simplifications are beneficial.
Advanced Concepts Related to Fraction Simplification
The principles of fraction simplification extend into more advanced mathematical concepts:
-
Prime Factorization: Finding the GCD can be facilitated by using prime factorization. This involves breaking down the numbers into their prime factors (numbers only divisible by 1 and themselves). The common prime factors are used to find the GCD. For 4 and 6, 4 = 2 x 2 and 6 = 2 x 3. The common factor is 2.
-
Rational Numbers: Fractions represent rational numbers – numbers that can be expressed as a ratio of two integers. Simplification helps to express rational numbers in their most concise form.
-
Algebraic Fractions: The same principle of simplification applies to algebraic fractions (fractions involving variables). The process involves factoring the numerator and denominator to find common factors that can be cancelled.
Conclusion: Mastering the Art of Fraction Simplification
Simplifying fractions is a fundamental mathematical skill with far-reaching applications. While the simplest form of 4/6 is 2/3, the process of arriving at this answer highlights the importance of understanding equivalent fractions, GCD, and the broader concepts related to rational numbers. Mastering this seemingly simple task provides a strong foundation for more complex mathematical concepts and enhances problem-solving capabilities in various fields. It's a skill that will serve you well throughout your life, from everyday tasks to more advanced academic pursuits. The ability to accurately and efficiently simplify fractions is a testament to a strong grasp of fundamental mathematical principles.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Simplest Form Of 4/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.