What Is The Slope Of The Line 3x 9y 4
News Co
Mar 31, 2025 · 5 min read
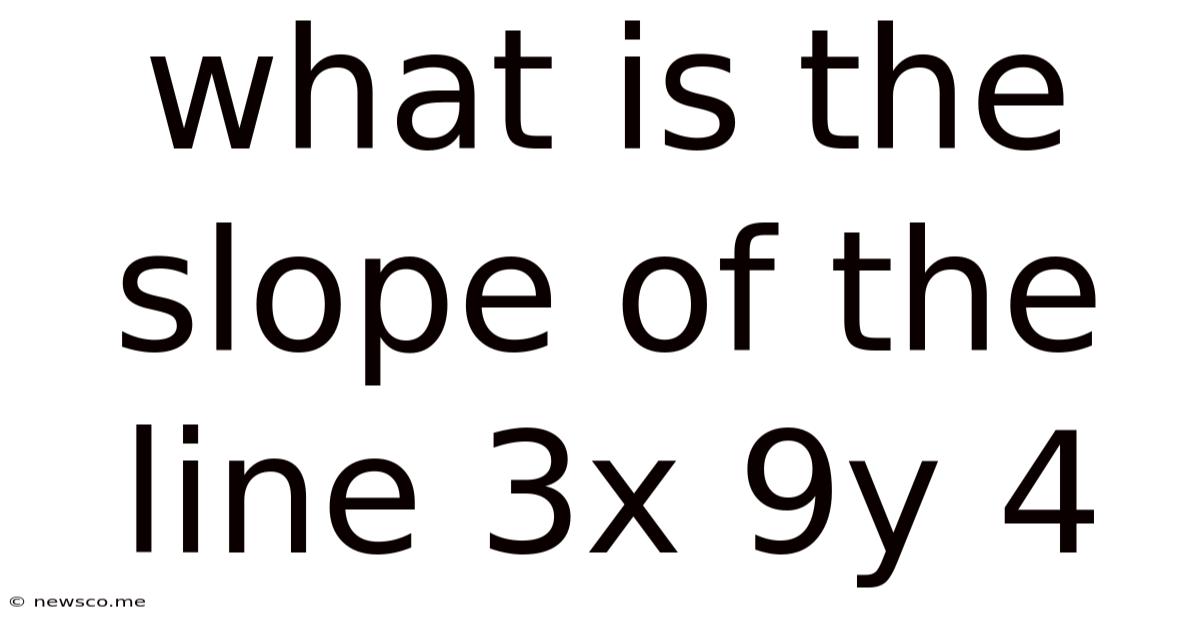
Table of Contents
What is the Slope of the Line 3x + 9y = 4? A Comprehensive Guide
Finding the slope of a line is a fundamental concept in algebra and geometry. This guide will thoroughly explain how to determine the slope of the line represented by the equation 3x + 9y = 4, covering various methods and related concepts. We'll also delve into the significance of slope and its applications.
Understanding the Slope-Intercept Form
Before we tackle the equation 3x + 9y = 4, let's review the slope-intercept form of a linear equation. This form is written as:
y = mx + b
Where:
- y represents the y-coordinate of a point on the line.
- x represents the x-coordinate of a point on the line.
- m represents the slope of the line.
- b represents the y-intercept (the point where the line crosses the y-axis).
The slope, m, tells us the steepness and direction of the line. A positive slope indicates an upward trend from left to right, while a negative slope indicates a downward trend. A slope of zero means the line is horizontal, and an undefined slope indicates a vertical line.
Calculating the Slope from the Given Equation
The equation 3x + 9y = 4 is not in slope-intercept form. To find the slope, we need to rearrange the equation to isolate y. Let's follow these steps:
-
Subtract 3x from both sides:
9y = -3x + 4
-
Divide both sides by 9:
y = (-3/9)x + (4/9)
-
Simplify the fraction:
y = (-1/3)x + (4/9)
Now, the equation is in slope-intercept form (y = mx + b). We can clearly see that the slope, m, is -1/3.
Understanding the Significance of the Slope (-1/3)
The slope of -1/3 tells us several things about the line:
- Negative Slope: The negative sign indicates that the line slopes downwards from left to right.
- Steepness: The fraction 1/3 indicates the ratio of the vertical change to the horizontal change. For every 3 units the line moves to the right along the x-axis, it moves down 1 unit along the y-axis.
Alternative Methods for Finding the Slope
While converting to slope-intercept form is the most straightforward method, let's explore other approaches to determine the slope:
Using Two Points on the Line
If we know two points that lie on the line, we can calculate the slope using the following formula:
m = (y2 - y1) / (x2 - x1)
Where:
- (x1, y1) and (x2, y2) are the coordinates of the two points.
To use this method, we need to find two points that satisfy the equation 3x + 9y = 4. Let's find two such points:
- If x = 0: 3(0) + 9y = 4 => 9y = 4 => y = 4/9. So, one point is (0, 4/9).
- If y = 0: 3x + 9(0) = 4 => 3x = 4 => x = 4/3. So, another point is (4/3, 0).
Now, let's apply the slope formula:
m = (0 - 4/9) / (4/3 - 0) = (-4/9) / (4/3) = (-4/9) * (3/4) = -1/3
As expected, we get the same slope, -1/3.
Using the Standard Form of a Linear Equation
The equation 3x + 9y = 4 is in the standard form of a linear equation, Ax + By = C. While not directly giving us the slope, we can derive it. The slope in standard form is given by:
m = -A / B
In our equation, A = 3 and B = 9. Therefore:
m = -3 / 9 = -1/3
Again, we obtain the same slope, -1/3.
Applications of Slope in Real-World Scenarios
The concept of slope is not limited to abstract mathematical problems. It has numerous real-world applications:
-
Engineering: Slope is crucial in civil engineering for calculating the gradient of roads, ramps, and other structures. Understanding slope ensures the safety and functionality of these constructions.
-
Physics: In physics, slope represents the rate of change of a quantity. For example, the slope of a velocity-time graph represents acceleration.
-
Economics: In economics, slope can represent the marginal rate of substitution or the relationship between two economic variables.
-
Data Analysis: In data analysis, the slope of a regression line indicates the relationship between two variables. A steeper slope implies a stronger relationship.
-
Computer Graphics: In computer graphics, slope is used to determine the direction and steepness of lines and curves, essential for creating realistic images and animations.
-
Geography: Slope is used in topography to describe the steepness of terrain and create contour maps.
Further Exploration: Parallel and Perpendicular Lines
Understanding slope helps us determine the relationship between different lines:
-
Parallel Lines: Parallel lines have the same slope. Any line parallel to 3x + 9y = 4 will also have a slope of -1/3.
-
Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. The negative reciprocal of -1/3 is 3. Therefore, any line perpendicular to 3x + 9y = 4 will have a slope of 3.
Conclusion: Mastering the Slope Concept
This comprehensive guide has demonstrated how to find the slope of the line 3x + 9y = 4 using various methods. We've emphasized the significance of the slope (-1/3) and explored its applications in diverse fields. Mastering the concept of slope is crucial for a solid understanding of linear equations and their real-world implications. By understanding slope, you can interpret linear relationships, analyze data, and solve problems across multiple disciplines. Remember to practice these methods with different equations to solidify your understanding. The more you practice, the more intuitive the process of finding and interpreting slopes will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Slope Of The Line 3x 9y 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.