What Is The Sqaure Root Of 4
News Co
Apr 06, 2025 · 6 min read
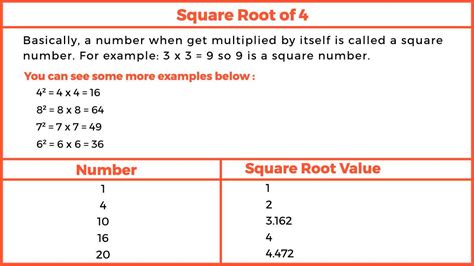
Table of Contents
What is the Square Root of 4? A Deep Dive into Basic Arithmetic
The seemingly simple question, "What is the square root of 4?" opens a door to a fascinating exploration of fundamental mathematical concepts. While the answer itself is straightforward – 2 – understanding the underlying principles and exploring its implications reveals a much richer mathematical landscape. This article will delve into the square root of 4, examining its calculation, its significance in various mathematical fields, and its broader applications in real-world scenarios.
Understanding Square Roots
Before we delve into the specifics of the square root of 4, let's establish a foundational understanding of square roots. A square root of a number is a value that, when multiplied by itself, gives the original number. In simpler terms, it's the inverse operation of squaring a number. For instance, if we square 3 (3 x 3 = 9), then the square root of 9 is 3. This can be represented mathematically as:
√9 = 3
This symbol, √, is the radical symbol, indicating the square root operation.
Calculating the Square Root of 4
Now, let's focus on the core question: What is the square root of 4? The answer is straightforward:
√4 = 2
This is because 2 multiplied by itself (2 x 2) equals 4.
However, it's crucial to note that while 2 is the principal square root, there is another valid solution in the realm of complex numbers. We'll explore this further below.
Beyond the Principal Square Root: Exploring Complex Numbers
While the principal square root of 4 is 2, the equation x² = 4 actually has two solutions: 2 and -2. This is because (-2) x (-2) also equals 4. This concept introduces the concept of complex numbers, which extends the number system beyond real numbers to include imaginary numbers. The imaginary unit, denoted by 'i', is defined as the square root of -1 (i² = -1).
While the square root of 4 within the realm of real numbers is solely 2, the complete solution set in the complex number system encompasses both 2 and -2.
The Importance of Context
The relevance of considering both solutions (2 and -2) depends entirely on the context of the problem. In many elementary mathematical applications, the principal square root (2) is sufficient. However, in more advanced mathematical contexts like quadratic equations or complex number analysis, both solutions are critical for a complete and accurate solution.
Applications of the Square Root of 4 and Related Concepts
The concept of square roots, including the square root of 4, has wide-ranging applications across various fields:
1. Geometry and Measurement
Square roots are fundamental in geometry, especially when dealing with calculating distances, areas, and volumes. Consider the Pythagorean theorem, a cornerstone of geometry: a² + b² = c². This theorem relates the lengths of the sides of a right-angled triangle. To find the length of the hypotenuse (c), one needs to use the square root. For example, if a = 2 and b = 2, then c = √(2² + 2²) = √8. While this doesn't directly involve the square root of 4, it highlights the importance of square roots in geometric calculations. Many geometric problems relating to squares, circles, and other shapes fundamentally involve square roots.
2. Physics and Engineering
Square roots are frequently used in physics and engineering calculations. For instance, calculating velocity, acceleration, and other physical quantities often involves square roots. Newton's Law of Universal Gravitation uses square roots in its equation, while calculations involving energy and momentum in various physics branches heavily rely on square root operations. In engineering, structural calculations, circuit analysis, and signal processing often involve solving equations which require the calculation of square roots.
3. Data Analysis and Statistics
Square roots appear in statistical calculations, particularly in determining standard deviations and variances. Standard deviation, a measure of data dispersion, involves calculating the square root of the variance. This plays a vital role in understanding the spread and distribution of data, useful in various fields ranging from finance to public health.
4. Computer Science and Programming
Square roots are essential in computer graphics, game development, and algorithm design. Many algorithms utilize square root calculations for tasks such as distance calculations, collision detection, and rendering three-dimensional environments. Programming languages include built-in functions for computing square roots, reflecting their importance in computational tasks.
5. Everyday Life
While not always explicitly stated, square roots permeate our daily lives. Consider simple activities like calculating the diagonal distance across a square room. The calculation depends on the Pythagorean theorem, requiring the use of square roots. The design of various objects and structures incorporates principles that rely on mathematical concepts which utilise square root calculations.
Advanced Concepts Related to Square Roots
The exploration of square roots extends beyond basic arithmetic, leading to more complex concepts:
1. nth Roots: Beyond Square Roots
While we focused on square roots (2nd roots), the concept extends to nth roots. The cube root (3rd root), for example, is a value that when multiplied by itself three times results in the original number. Similarly, you can have fourth roots, fifth roots, and so on. These higher-order roots are equally important in various advanced mathematical fields.
2. Irrational Numbers: The Nature of Square Roots
The square root of many numbers are irrational numbers – numbers that cannot be expressed as a simple fraction. For example, the square root of 2 (√2) is an irrational number, as it cannot be expressed as a fraction of two integers. Understanding the concept of irrational numbers is crucial to understanding the nature of square roots.
3. Solving Quadratic Equations
Quadratic equations (equations of the form ax² + bx + c = 0) are frequently solved using the quadratic formula, which involves the square root operation. Understanding this relationship is critical in solving many algebraic problems.
4. Calculus and Advanced Mathematics
Square roots and related concepts play crucial roles in calculus, especially in dealing with derivatives and integrals. The concepts underpin various more advanced mathematical theories and applications.
Conclusion: The Significance of the Simple Square Root
While the square root of 4 might seem like a trivial mathematical problem, its exploration reveals the richness and depth of fundamental mathematical concepts. From basic arithmetic to advanced calculus and its widespread applications in various scientific and technical fields, the concept of square roots remains an indispensable tool for understanding and solving a wide range of problems in the world around us. The seemingly simple answer of 2 holds within it a gateway to a deeper understanding of mathematics and its profound impact on our lives. Further exploration of these concepts will undoubtedly lead to a greater appreciation of the beauty and power of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Sqaure Root Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.