What Is The Squar Root Of 81
News Co
Apr 05, 2025 · 5 min read
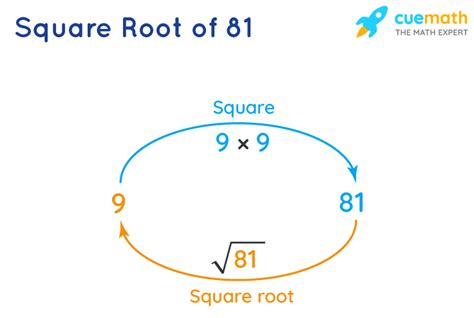
Table of Contents
What is the Square Root of 81? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What is the square root of 81?" opens the door to a fascinating world of mathematics, encompassing fundamental concepts, practical applications, and even historical context. While the answer itself is straightforward – 9 – understanding the underlying principles and exploring the broader implications of square roots significantly enriches our mathematical literacy. This article will delve into the intricacies of square roots, exploring what they are, how they're calculated, and where they appear in various fields.
Understanding Square Roots: The Basics
A square root is a number that, when multiplied by itself, produces a given number. In simpler terms, it's the inverse operation of squaring a number. For example, the square of 9 (9²) is 81 (9 x 9 = 81), therefore, the square root of 81 (√81) is 9.
Key Terminology:
- Square: The result of multiplying a number by itself (e.g., 9² = 81).
- Square Root: A number that, when multiplied by itself, equals a given number (e.g., √81 = 9).
- Radical Symbol (√): The symbol used to denote a square root.
- Radicand: The number under the radical symbol (e.g., in √81, 81 is the radicand).
Why are Square Roots Important?
Square roots are fundamental to many areas of mathematics and beyond. They are essential for:
- Solving Quadratic Equations: Many real-world problems, from physics to engineering, involve solving quadratic equations (equations of the form ax² + bx + c = 0), and square roots are crucial for finding the solutions.
- Geometry and Trigonometry: Calculating distances, areas, and volumes often requires the use of square roots, particularly in problems involving right-angled triangles (Pythagorean theorem).
- Statistics: Standard deviation, a key measure of data dispersion, involves calculating square roots.
- Physics: Numerous physical phenomena, like calculating velocity or energy, involve square roots in their formulas.
- Computer Graphics: Square roots are used extensively in computer graphics and game development for calculations related to 3D transformations, lighting, and shading.
Calculating the Square Root of 81 and Other Numbers
While the square root of 81 is easily recognizable as 9, finding the square root of other numbers might require different methods. Let's explore some common techniques:
1. Memorization:
For smaller, perfect squares like 81, 16, 25, etc., memorizing their square roots is highly efficient. This allows for quick calculations in various contexts.
2. Prime Factorization:
This method is particularly useful for larger numbers. It involves breaking down the number into its prime factors. For instance, to find the square root of 144:
- Prime Factorization: 144 = 2 x 2 x 2 x 2 x 3 x 3 = 2⁴ x 3²
- Pairing Factors: Notice the pairs of identical prime factors (2 x 2 and 3 x 3).
- Square Root: Take one factor from each pair and multiply them: 2 x 3 = 6. Therefore, √144 = 6.
This method works well for perfect squares but can be less efficient for non-perfect squares.
3. Estimation:
For numbers that aren't perfect squares, estimation is a valuable skill. For example, to estimate the square root of 70:
- Identify Nearest Perfect Squares: The nearest perfect squares to 70 are 64 (8²) and 81 (9²).
- Approximate: Since 70 is closer to 64 than 81, the square root of 70 is likely slightly greater than 8. A closer approximation might be around 8.3 or 8.4.
4. Using a Calculator:
Calculators offer the most straightforward method for finding square roots, providing precise results for any non-negative number.
Beyond the Square Root of 81: Exploring Higher Roots
While we've primarily focused on square roots, mathematics extends to higher-order roots like cube roots (∛), fourth roots (∜), and so on. These represent numbers that, when multiplied by themselves a certain number of times, equal the given number. For instance:
- Cube root of 8 (∛8): This is 2, because 2 x 2 x 2 = 8.
- Fourth root of 16 (∜16): This is 2, because 2 x 2 x 2 x 2 = 16.
Higher-order roots are used in various advanced mathematical fields and have applications in areas like engineering and physics.
The Square Root of Negative Numbers: Imaginary Numbers
A critical aspect of square roots involves the concept of imaginary numbers. The square root of a negative number, like √-1, cannot be expressed as a real number because no real number multiplied by itself results in a negative number. To address this, mathematicians introduced the imaginary unit, denoted as "i," where i² = -1. This allows for the calculation of square roots of negative numbers, expanding the realm of mathematics into the complex number system (numbers with both real and imaginary components).
Real-World Applications: Where Square Roots Matter
The seemingly abstract concept of square roots has significant practical applications across various disciplines:
1. Engineering and Physics:
Square roots are fundamental to numerous engineering calculations, including:
- Structural Engineering: Calculating forces and stresses in buildings and bridges.
- Electrical Engineering: Working with impedance and power calculations in electrical circuits.
- Mechanical Engineering: Determining velocities and accelerations in mechanical systems.
2. Finance:
Square roots are used in financial models:
- Standard Deviation: Measuring the risk associated with investment portfolios.
- Option Pricing: Calculating the value of financial options using complex mathematical models.
3. Computer Science:
Square roots are extensively utilized in:
- Computer Graphics: Rendering 3D images and animations.
- Game Development: Calculating distances and positions of objects in virtual environments.
- Algorithm Design: Developing efficient algorithms for various computations.
4. Medicine:
Square roots find applications in medical fields such as:
- Statistical Analysis: Analyzing clinical trial data.
- Medical Imaging: Processing and interpreting images from medical scans.
Conclusion: The Enduring Significance of Square Roots
The seemingly simple question of the square root of 81 unravels into a vast and fascinating mathematical concept with profound implications across various fields. From solving quadratic equations to calculating distances in geometry, and from understanding statistical measures to designing complex engineering systems, square roots are an integral part of our world. Understanding their fundamental principles, various methods of calculation, and diverse applications empowers us to appreciate the beauty and utility of mathematics in our everyday lives. The seemingly simple answer, 9, represents a gateway to a rich and rewarding mathematical journey.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Squar Root Of 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.