What Is The Square Root 289
News Co
Apr 06, 2025 · 5 min read
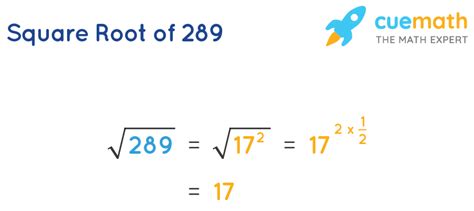
Table of Contents
What is the Square Root of 289? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What is the square root of 289?" opens a door to a fascinating world of mathematics, encompassing fundamental concepts, practical applications, and even historical context. While a calculator readily provides the answer, understanding the why behind the answer is far more enriching. This article will explore the square root of 289, delve into the broader concept of square roots, and examine their relevance in various fields.
Understanding Square Roots
Before we tackle the square root of 289 specifically, let's establish a solid understanding of what a square root actually is. In essence, the square root of a number is a value that, when multiplied by itself (squared), equals the original number. For instance, the square root of 9 is 3 because 3 * 3 = 9. This can be expressed mathematically as √9 = 3. The symbol '√' is the radical symbol, indicating the square root operation.
Key Concepts:
-
Perfect Squares: Numbers that are the result of squaring an integer (e.g., 9, 16, 25, 289) are called perfect squares. Finding the square root of a perfect square yields an integer result.
-
Non-Perfect Squares: Numbers that are not the result of squaring an integer (e.g., 2, 7, 10) are non-perfect squares. The square roots of these numbers are irrational numbers—numbers that cannot be expressed as a simple fraction and have decimal representations that go on forever without repeating.
-
Principal Square Root: Every positive number has two square roots: one positive and one negative. However, the principal square root is the non-negative square root. For example, while both 3 and -3 squared equal 9, the principal square root of 9 is 3.
Calculating the Square Root of 289
Now, let's return to our original question: What is the square root of 289? We're looking for a number that, when multiplied by itself, equals 289. There are several ways to approach this:
1. Using a Calculator: The simplest method is to use a calculator. Inputting √289 into a calculator will instantly provide the answer: 17.
2. Prime Factorization: A more mathematical approach involves prime factorization. We break down 289 into its prime factors:
289 = 17 x 17
Since 289 is a perfect square (17 x 17), its square root is simply 17.
3. Manual Estimation and Iteration (Newton-Raphson Method): For larger numbers, a more sophisticated method like the Newton-Raphson method can be used to approximate the square root through iterative calculations. While this method is more complex and beyond the scope of this introductory explanation, it highlights the mathematical power behind calculating square roots.
The Significance of 17 (√289)
The fact that the square root of 289 is 17 has implications beyond its simple numerical value. 17 is a prime number, meaning it's only divisible by 1 and itself. Prime numbers play a crucial role in cryptography and other areas of computer science. Understanding the square root of 289 contributes to a broader mathematical understanding and skillset.
Applications of Square Roots
Square roots are not merely abstract mathematical concepts; they have extensive practical applications across various disciplines:
1. Geometry: Square roots are fundamental in geometry. Calculating the length of the hypotenuse of a right-angled triangle using the Pythagorean theorem (a² + b² = c²) inherently involves finding a square root. This is crucial in surveying, construction, and engineering.
2. Physics: Square roots appear frequently in physics, particularly in calculations involving velocity, acceleration, and energy. For instance, calculating the speed of an object requires the square root of its kinetic energy.
3. Finance: Square roots are used in financial calculations, such as determining standard deviation and variance in investment portfolios. These calculations help assess risk and optimize investment strategies.
4. Computer Graphics: Square roots are vital in computer graphics and game development. They're used in calculations related to distance, scaling, and transformations of objects within a 3D space.
5. Statistics: In statistics, the square root is used in various calculations, including the calculation of standard deviation, which measures the dispersion of a dataset. This is crucial for data analysis and interpretation.
6. Engineering: Square roots are used extensively in civil, electrical, and mechanical engineering for calculations involving structural integrity, electrical circuits, and mechanical systems.
Beyond Square Roots: Higher-Order Roots
The concept of square roots extends to higher-order roots. A cube root (∛) is a number that, when multiplied by itself three times, equals the original number. Similarly, a fourth root, fifth root, and so on can be defined. These higher-order roots find applications in more advanced mathematical and scientific fields.
Historical Context of Square Roots
The concept of square roots has a rich history, dating back to ancient civilizations. Babylonian mathematicians, as early as 1800 BC, developed sophisticated methods for approximating square roots. The Greeks also made significant contributions to the understanding of square roots, with Euclid's Elements providing a rigorous geometrical treatment of the concept. The development of modern algebraic notation greatly simplified the representation and calculation of square roots.
Conclusion: The Enduring Importance of Understanding Square Roots
While a calculator can readily provide the answer to "What is the square root of 289?", the journey to understanding the underlying mathematical principles and practical applications is far more rewarding. The square root of 289, being 17, is not just a numerical value; it's a gateway to a deeper understanding of mathematics, its historical development, and its widespread relevance in various fields. This understanding is invaluable not only for students pursuing mathematical studies but also for anyone seeking a more profound grasp of the world around them. The ability to grasp and apply the concept of square roots empowers individuals with critical thinking and problem-solving skills applicable across numerous disciplines. The seemingly simple question, therefore, unlocks a treasure trove of knowledge and skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Square Root 289 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.