What Is The Square Root Of 110
News Co
Apr 08, 2025 · 4 min read
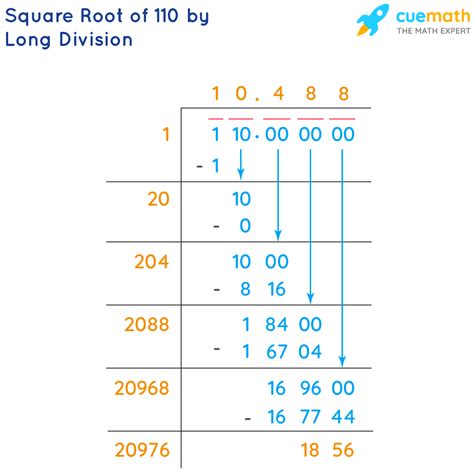
Table of Contents
What is the Square Root of 110? A Deep Dive into Approximation and Calculation
The question, "What is the square root of 110?" seems simple enough. However, exploring this seemingly straightforward mathematical problem opens doors to a fascinating world of approximation techniques, numerical methods, and the underlying properties of irrational numbers. Let's delve into this seemingly simple question and uncover its complexities.
Understanding Square Roots
Before we tackle the square root of 110 specifically, let's refresh our understanding of square roots. The square root of a number x is a value that, when multiplied by itself, equals x. In mathematical notation, this is represented as √x. For example, √9 = 3 because 3 * 3 = 9.
Finding the square root of perfect squares (numbers that are the product of an integer multiplied by itself) is straightforward. However, most numbers, including 110, are not perfect squares. This means their square roots are irrational numbers – numbers that cannot be expressed as a simple fraction and have decimal representations that go on forever without repeating.
Approximating the Square Root of 110
Since 110 isn't a perfect square, we need to employ approximation techniques to find its square root. Several methods exist, each with varying levels of accuracy and complexity:
1. Estimation using Perfect Squares
The simplest method involves estimating based on nearby perfect squares. We know that 10² = 100 and 11² = 121. Since 110 lies between 100 and 121, its square root must be between 10 and 11. A reasonable initial guess would be somewhere around 10.5.
This method provides a rough estimate, but it lacks precision. For more accurate approximations, we need more sophisticated techniques.
2. The Babylonian Method (or Heron's Method)
The Babylonian method, also known as Heron's method, is an iterative algorithm that refines an initial guess to progressively improve accuracy. The formula is:
x_(n+1) = 0.5 * (x_n + S/x_n)
where:
- x_n is the current approximation
- x_(n+1) is the next, improved approximation
- S is the number whose square root we're seeking (in our case, 110)
Let's use an initial guess of 10.5:
- Iteration 1: x_1 = 0.5 * (10.5 + 110/10.5) ≈ 10.488
- Iteration 2: x_2 = 0.5 * (10.488 + 110/10.488) ≈ 10.488
- The method converges quickly, and further iterations yield minimal changes.
Therefore, using the Babylonian method, we can approximate the square root of 110 as approximately 10.488.
3. Using a Calculator or Computer Software
Modern calculators and computer software readily provide the square root of any number. Using a calculator, we find that the square root of 110 is approximately 10.4880884817. This level of precision is far beyond what we could achieve through manual approximation methods.
Deeper Dive into Irrational Numbers
The square root of 110, like most square roots of non-perfect squares, is an irrational number. This means its decimal representation is non-terminating and non-repeating. Understanding this characteristic is crucial for appreciating the limitations of approximation techniques. No matter how many decimal places we calculate, we'll never reach the exact value. We can only get increasingly closer approximations.
Applications of Square Roots
Understanding square roots is fundamental to various mathematical and scientific fields. Here are a few applications:
- Geometry: Calculating distances, areas, and volumes frequently involves square roots, particularly in the Pythagorean theorem (a² + b² = c²), where finding the length of the hypotenuse requires calculating a square root.
- Physics: Many physics equations, particularly those dealing with motion, energy, and waves, incorporate square roots.
- Statistics: Standard deviation, a crucial measure of data dispersion, uses square roots in its calculation.
- Engineering: Square roots are essential for solving problems related to stress, strain, and other engineering concepts.
Beyond the Basics: Advanced Techniques
For extremely high-precision calculations, more advanced numerical methods are employed. These methods include:
- Newton-Raphson Method: A powerful iterative method for finding roots of equations, including square roots.
- Taylor Series Expansion: This method approximates functions using infinite series, providing highly accurate approximations for square roots.
Conclusion: The Square Root of 110 and Beyond
While the simple answer to "What is the square root of 110?" might seem to be a single numerical value obtainable from a calculator, a deeper exploration reveals the rich mathematical concepts underlying the calculation. Understanding approximation techniques, the nature of irrational numbers, and the broader applications of square roots provides a much more comprehensive understanding of this seemingly simple problem. This exploration highlights the beauty and complexity found even within fundamental mathematical concepts. From simple estimation to sophisticated numerical methods, the quest for the square root of 110 offers a valuable journey into the world of mathematics. The journey itself, and the understanding gained along the way, are as important as the final, approximate answer.
Latest Posts
Latest Posts
-
Whats The Square Root Of 64
Apr 08, 2025
-
What Is L V In Roman Numerals
Apr 08, 2025
-
Whats The Square Root Of 22
Apr 08, 2025
-
How To Work Out The Area Of A Trapezium
Apr 08, 2025
-
Half Of 3 8 On A Tape Measure
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 110 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.