What Is The Square Root Of 208
News Co
Apr 05, 2025 · 5 min read
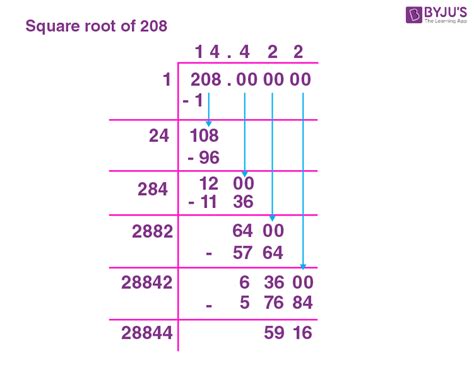
Table of Contents
What is the Square Root of 208? A Deep Dive into Square Roots and Their Applications
The question, "What is the square root of 208?" might seem simple at first glance. However, delving into this seemingly straightforward query opens up a fascinating exploration of mathematical concepts, their practical applications, and the nuances of numerical computation. This article will not only answer the question directly but also provide a comprehensive understanding of square roots, their properties, and their relevance in various fields.
Understanding Square Roots
Before we tackle the square root of 208, let's establish a firm grasp on the fundamental concept. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. We represent this mathematically as √9 = 3.
This seemingly simple operation has far-reaching implications in various branches of mathematics, science, and engineering. It's a cornerstone of algebra, geometry, trigonometry, and even physics.
Calculating the Square Root of 208
208 isn't a perfect square – meaning there's no whole number that, when multiplied by itself, equals 208. Therefore, the square root of 208 will be an irrational number, a number that cannot be expressed as a simple fraction. It will have an infinite number of decimal places that do not repeat in a pattern.
To find the approximate value, we can use several methods:
-
Using a calculator: The most straightforward method is to use a calculator. Simply input √208, and the calculator will provide the approximate value, which is approximately 14.4222051.
-
Prime Factorization: We can simplify the square root by finding the prime factors of 208. The prime factorization of 208 is 2³ x 13. Therefore, √208 can be simplified to √(2³ x 13) = √(2² x 2 x 13) = 2√(2 x 13) = 2√26. This simplifies the calculation somewhat, but we still need a calculator or approximation methods to find the decimal value of √26.
-
Newton's Method (Iterative Method): For those interested in numerical methods, Newton's method provides an iterative approach to finding increasingly accurate approximations of square roots. It involves an iterative formula that refines the estimate with each step. While beyond the scope of a simple explanation here, it's a powerful technique used in computer algorithms for calculating square roots.
The Significance of Irrational Numbers
The fact that the square root of 208 is an irrational number highlights the richness of the number system. Irrational numbers, though not easily represented as fractions, are essential components of mathematical calculations and real-world applications. They constantly appear in geometry, particularly when dealing with lengths and areas of figures. The diagonal of a square, for instance, is always an irrational number unless the sides are zero.
Applications of Square Roots in Real-World Scenarios
Square roots are not merely abstract mathematical concepts; they have numerous practical applications across diverse fields:
-
Physics: Calculating velocities, accelerations, and distances in projectile motion problems often requires the use of square roots. The Pythagorean theorem, which uses square roots, is crucial in various physics calculations, including determining the magnitude of vectors.
-
Engineering: Civil engineers use the Pythagorean theorem extensively in calculations related to bridge construction, building design, and surveying. Mechanical engineers utilize square roots in calculating forces, stresses, and strains in structures and machinery.
-
Finance: Compound interest calculations involve the use of square roots. Financial models often rely on square root functions for determining risk and volatility in investments.
-
Computer Graphics: Square roots play a critical role in generating graphics and animations. They are integral to calculations involving distances, rotations, and transformations in 2D and 3D graphics.
-
Statistics: Standard deviation, a key measure of data dispersion, involves the calculation of a square root. Understanding standard deviation is crucial in analyzing data sets and drawing conclusions.
-
Navigation: The calculation of distances and bearings using latitude and longitude coordinates involves the use of square roots. This is particularly important in GPS systems and navigation applications.
Beyond the Square Root of 208: Exploring Further
While we've focused on the square root of 208, the underlying principles and applications extend to all square roots. Understanding square roots is a gateway to exploring more advanced mathematical concepts, such as:
-
Higher-order roots: Cube roots, fourth roots, and nth roots are generalizations of the square root concept. These are vital in various fields, including solving polynomial equations and advanced mathematical modeling.
-
Complex numbers: Square roots of negative numbers lead to the concept of imaginary numbers and complex numbers, which are indispensable in electrical engineering, quantum mechanics, and signal processing.
-
Approximation techniques: Exploring different methods for approximating square roots, like the Babylonian method or the Newton-Raphson method, provides deeper insights into numerical analysis and computational algorithms.
Conclusion
The simple question of "What is the square root of 208?" unfolds into a rich and fascinating exploration of mathematical concepts and their profound implications. The approximate value, 14.4222051, is merely the tip of the iceberg. Understanding the underlying principles, the significance of irrational numbers, and the diverse applications of square roots equips us with a more profound appreciation for the power and utility of mathematics in our world. The seemingly mundane calculation becomes a gateway to a deeper understanding of the mathematical universe and its impact on our daily lives. This exploration highlights the importance of continuous learning and critical thinking in unraveling the complexities of the mathematical world. By understanding the fundamental concepts and their applications, we can unlock a deeper appreciation for the beauty and utility of mathematics. The seemingly simple question of the square root of 208 ultimately serves as a powerful reminder of the intricate interconnectedness of mathematics and its pervasive influence across various disciplines and aspects of modern life.
Latest Posts
Latest Posts
-
Is 0 A Multiple Of 3
Apr 06, 2025
-
What Is The Vertical Angles Theorem
Apr 06, 2025
-
What Is The 10 Percent Of 500
Apr 06, 2025
-
What Is The Least Common Multiple Of 9 And 18
Apr 06, 2025
-
Least Common Multiple Of 7 And 4
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 208 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
