What Is The Square Root Of 244
News Co
Apr 05, 2025 · 5 min read
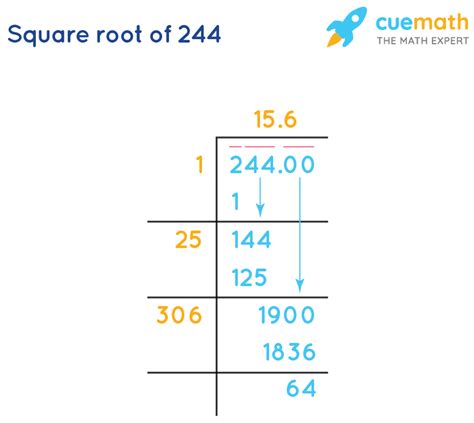
Table of Contents
What is the Square Root of 244? A Deep Dive into Square Roots and Numerical Approximation
The seemingly simple question, "What is the square root of 244?" opens a door to a fascinating exploration of mathematics, encompassing fundamental concepts, approximation techniques, and the power of numerical methods. While a calculator readily provides a decimal approximation, understanding the underlying principles offers a richer appreciation of the mathematical world. This article will delve into the intricacies of finding the square root of 244, examining both exact and approximate solutions, and exploring related mathematical concepts.
Understanding Square Roots
Before we tackle the square root of 244, let's establish a foundational understanding of what a square root represents. The square root of a number, 'x', is a value that, when multiplied by itself, equals 'x'. In mathematical notation, this is represented as √x. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9.
Key Concepts:
- Perfect Squares: Numbers that are the result of squaring an integer (e.g., 9, 16, 25) are called perfect squares. Their square roots are whole numbers.
- Non-Perfect Squares: Numbers that are not the result of squaring an integer (e.g., 2, 3, 244) are non-perfect squares. Their square roots are irrational numbers – numbers that cannot be expressed as a simple fraction. They have infinite, non-repeating decimal expansions.
- Irrational Numbers: Numbers like π (pi) and the square root of most non-perfect squares are irrational. They cannot be expressed as a ratio of two integers.
Finding the Square Root of 244: The Approach
244 is not a perfect square. Therefore, its square root will be an irrational number. We can't express it exactly as a fraction or a terminating decimal. However, we can find increasingly accurate approximations.
1. Prime Factorization
A helpful first step, particularly for understanding the nature of the number, is to perform prime factorization. This breaks down the number into its prime number components.
244 = 2 x 2 x 61 = 2² x 61
This factorization reveals that 244 has a perfect square factor (2²). This allows a degree of simplification.
2. Simplifying the Square Root
Using the properties of square roots, we can simplify the expression:
√244 = √(2² x 61) = √2² x √61 = 2√61
This simplified form shows that the square root of 244 is equal to 2 times the square root of 61. While this doesn't provide a decimal value, it's a more concise and mathematically accurate representation.
3. Numerical Approximation Methods
To obtain a decimal approximation, we can employ several numerical methods. Here are a few common techniques:
-
Babylonian Method (or Heron's Method): This iterative method refines an initial guess to get progressively closer to the actual square root. The formula is:
x_(n+1) = 0.5 * (x_n + 244/x_n)
Where:
- x_n is the current guess
- x_(n+1) is the improved guess
Starting with an initial guess (e.g., 15), repeated application of this formula yields increasingly accurate approximations.
-
Newton-Raphson Method: A more sophisticated iterative method, similar in concept to the Babylonian method, but often converging faster.
-
Calculator/Software: Modern calculators and mathematical software packages provide highly accurate approximations directly.
4. Using a Calculator
The simplest approach is to use a calculator or computer software. These tools employ advanced algorithms to calculate the square root to a high degree of precision. The approximate value is typically:
√244 ≈ 15.6205
Exploring Related Mathematical Concepts
The quest to find the square root of 244 touches upon several broader mathematical concepts:
-
Irrational Numbers and Their Significance: The fact that the square root of 244 is irrational highlights the importance of irrational numbers in mathematics. They are fundamental to geometry, calculus, and many other advanced mathematical fields.
-
Number Systems: This exploration underscores the different number systems – natural numbers, integers, rational numbers, and irrational numbers – and how they relate to each other.
-
Iterative Methods and Numerical Analysis: The Babylonian and Newton-Raphson methods demonstrate the power of iterative methods in approximating solutions to problems that may not have exact analytical solutions. This is a core concept in numerical analysis.
-
Approximation and Error: When working with irrational numbers, we inevitably deal with approximations. Understanding the concept of error and how to minimize it is crucial in many scientific and engineering applications.
Practical Applications of Square Roots
Understanding and calculating square roots isn't just an academic exercise; it has practical applications across various fields:
-
Geometry: Calculating distances, areas, and volumes often involves square roots. For instance, finding the diagonal of a rectangle or the hypotenuse of a right-angled triangle uses the Pythagorean theorem, which involves square roots.
-
Physics: Many physical phenomena involve square roots, such as calculating velocity, acceleration, or energy.
-
Engineering: Square roots are essential in various engineering calculations, including structural design, electrical circuits, and fluid dynamics.
-
Computer Graphics: Rendering images and animations often requires extensive use of square roots for geometric calculations.
-
Finance: Square roots are used in financial modeling and risk assessment calculations.
Conclusion: Beyond the Calculation
The seemingly straightforward question, "What is the square root of 244?" has led us on a journey into the heart of mathematical concepts. While a calculator provides a quick decimal approximation (approximately 15.6205), understanding the underlying principles, the nature of irrational numbers, and the methods for approximating solutions offers a much deeper and more rewarding experience. The exploration has touched upon the elegance of prime factorization, the iterative nature of numerical approximation methods, and the profound significance of square roots in various fields. Remember, the true value lies not only in the answer itself but also in the journey of understanding the mathematical landscape it unveils. This understanding is key to applying these concepts effectively in various practical applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 244 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.