What Is The Square Root Of 340
News Co
Apr 07, 2025 · 5 min read
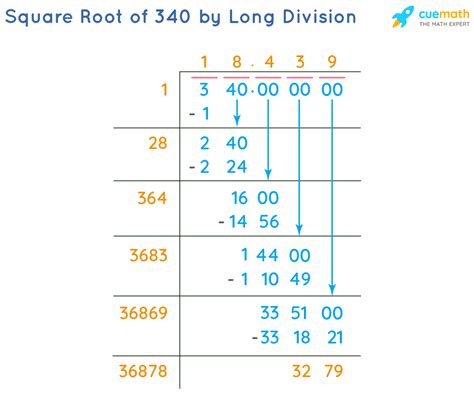
Table of Contents
What is the Square Root of 340? A Deep Dive into Square Roots and Numerical Approximation
The seemingly simple question, "What is the square root of 340?" opens a door to a fascinating exploration of mathematical concepts, numerical methods, and the practical applications of understanding square roots. While a calculator readily provides an approximate answer, understanding the underlying principles and methods for calculating square roots offers valuable insights into mathematics and its real-world relevance. This article delves into the square root of 340, exploring various approaches to find its value and highlighting the significance of this fundamental mathematical operation.
Understanding Square Roots
Before we tackle the square root of 340 specifically, let's establish a solid understanding of what a square root is. The square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. This is often represented mathematically as √9 = 3.
Key Concepts:
- Perfect Squares: Numbers that are the squares of integers (e.g., 4, 9, 16, 25) are called perfect squares. Their square roots are integers.
- Non-Perfect Squares: Numbers that are not perfect squares have irrational square roots. This means their decimal representation goes on forever without repeating. 340 is a non-perfect square.
- Principal Square Root: Every positive number has two square roots – a positive and a negative one. However, the principal square root is the non-negative square root. When we refer to "the square root," we typically mean the principal square root.
Methods for Approximating the Square Root of 340
Since 340 is not a perfect square, we need to use approximation methods to find its square root. Here are several approaches:
1. Using a Calculator
The simplest and most direct method is to use a calculator or computer software. Most calculators have a square root function (often denoted as √ or x<sup>1/2</sup>). Entering 340 and pressing the square root button will provide a close approximation. You'll find that the square root of 340 is approximately 18.4390889145.
2. Babylonian Method (Heron's Method)
The Babylonian method, also known as Heron's method, is an iterative algorithm that refines an initial guess to progressively approach the square root. It's based on the principle that if 'x' is an overestimate of the square root of a number 'n', then n/x will be an underestimate, and their average will be a better approximation.
Steps:
-
Make an initial guess: Start with a reasonable guess for the square root of 340. Since 18² = 324 and 19² = 361, a good starting point is 18.5.
-
Iterate: Apply the formula: Next guess = (Previous guess + n / Previous guess) / 2
-
Repeat: Repeat step 2 until the desired level of accuracy is achieved. The more iterations, the closer the approximation gets to the actual square root.
Let's perform a few iterations:
- Iteration 1: (18.5 + 340 / 18.5) / 2 ≈ 18.43956
- Iteration 2: (18.43956 + 340 / 18.43956) / 2 ≈ 18.4390889
- Iteration 3: Further iterations would yield even more precise results.
3. Linear Approximation
This method uses the tangent line of a function to approximate the value of the function at a specific point. For the square root function, we can use the tangent line at a nearby point whose square root is known.
Let's use the point (361, 19). The derivative of the square root function, f(x) = √x, is f'(x) = 1/(2√x). At x = 361, the derivative is 1/(2*19) = 1/38. The equation of the tangent line at (361, 19) is:
y - 19 = (1/38)(x - 361)
To approximate √340, let x = 340:
y - 19 = (1/38)(340 - 361) y ≈ 18.447
This method provides a less precise approximation than the Babylonian method, but it demonstrates a different mathematical approach.
4. Using Logarithms
Logarithms can be used to approximate square roots. The relationship between logarithms and square roots is based on the property that log(√x) = (1/2)log(x). Using logarithm tables or a calculator with logarithmic functions, we can perform the calculation:
- Find the logarithm of 340 (using base 10, for example).
- Divide the result by 2.
- Find the antilogarithm of the result.
This method, while mathematically sound, is less straightforward for manual calculation than the Babylonian method.
Significance and Applications of Square Roots
Understanding square roots is fundamental to various mathematical concepts and practical applications:
- Geometry: Calculating the lengths of sides of right-angled triangles using the Pythagorean theorem (a² + b² = c²) requires finding square roots. This has applications in surveying, construction, and engineering.
- Physics: Many physics formulas involve square roots, such as calculations related to velocity, acceleration, and energy.
- Statistics: Standard deviation, a crucial measure of data dispersion in statistics, involves calculating the square root of the variance.
- Computer Graphics: Square roots are used extensively in computer graphics and game development for calculations related to distances, rotations, and transformations.
- Finance: Square roots are utilized in financial models for calculations involving risk, variance, and portfolio optimization.
Conclusion: Beyond the Calculation
The square root of 340, while seemingly a simple numerical problem, illustrates the power and beauty of mathematics. It highlights various methods for approximating values and underscores the deep connections between fundamental mathematical concepts and their wide-ranging applications in various fields. Whether you're using a calculator for a quick result or employing iterative methods for a deeper understanding, the journey to finding the square root of 340 provides valuable insights into the heart of mathematical reasoning and its real-world significance. The approximate value of 18.439 serves not just as an answer, but as a gateway to a more profound appreciation of mathematics and its practical uses.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 340 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.