What Is The Square Root Of 512
News Co
Apr 05, 2025 · 5 min read
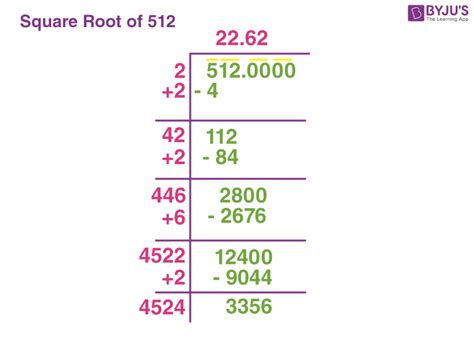
Table of Contents
What is the Square Root of 512? A Deep Dive into Square Roots and Their Applications
Finding the square root of a number is a fundamental concept in mathematics, with far-reaching applications across various fields. This article will delve into the specifics of calculating the square root of 512, exploring different methods, explaining the underlying principles, and showcasing the relevance of square roots in real-world scenarios.
Understanding Square Roots
Before we tackle the square root of 512, let's establish a solid understanding of what a square root is. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 (3²) equals 9. This is often represented mathematically as √9 = 3.
The square root of a number can be a whole number (integer), a fraction, or an irrational number (a number that cannot be expressed as a simple fraction). The square root of 512 falls into the latter category.
Calculating the Square Root of 512
Several methods exist for calculating the square root of 512. We'll explore the most common approaches:
1. Prime Factorization:
This method involves breaking down the number into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. The prime factorization of 512 is 2<sup>9</sup> (2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2).
Therefore:
√512 = √(2<sup>9</sup>) = √(2<sup>8</sup> x 2) = 2<sup>4</sup>√2 = 16√2
This means the square root of 512 is 16 times the square root of 2. Since √2 is an irrational number (approximately 1.414), the square root of 512 is also irrational.
2. Using a Calculator:
The simplest method is to use a calculator. Most scientific calculators have a square root function (√). Simply enter 512 and press the square root button. The calculator will provide an approximate decimal value, typically around 22.627. This is an approximation because, as established, √512 is an irrational number.
3. Babylonian Method (or Heron's Method):
This is an iterative method for approximating square roots. It starts with an initial guess and refines it through successive iterations. The formula is:
x<sub>n+1</sub> = ½ (x<sub>n</sub> + a/x<sub>n</sub>)
Where:
- x<sub>n</sub> is the current approximation
- x<sub>n+1</sub> is the next approximation
- a is the number whose square root is being calculated (512 in our case)
Let's illustrate with an initial guess of 20:
- x<sub>1</sub> = 20
- x<sub>2</sub> = ½ (20 + 512/20) ≈ 22.6
- x<sub>3</sub> = ½ (22.6 + 512/22.6) ≈ 22.627
Each iteration brings the approximation closer to the actual value. The Babylonian method is particularly useful when calculators aren't readily available.
4. Using Logarithms:
Logarithms can also be employed to calculate square roots. The following formula applies:
√a = 10<sup>(log a)/2</sup>
Where 'a' is the number whose square root is being calculated. Therefore:
√512 = 10<sup>(log 512)/2</sup>
This approach requires using logarithmic tables or a calculator with logarithmic functions.
The Significance of Irrational Numbers
The fact that the square root of 512 is an irrational number underscores the complexity and richness of the number system. Irrational numbers, although unending and non-repeating decimals, are essential components of mathematical calculations and have countless applications in real-world scenarios.
Real-World Applications of Square Roots
Square roots have widespread applications in numerous fields:
1. Geometry and Physics:
- Calculating distances: The Pythagorean theorem, a fundamental concept in geometry, utilizes square roots to calculate the length of the hypotenuse of a right-angled triangle (a² + b² = c²). This has implications in various fields like surveying, navigation, and construction.
- Calculating areas and volumes: Determining the area of a square or the volume of a cube involves taking the square root.
- Physics problems: Many physics equations involve square roots, especially those related to speed, velocity, acceleration, and energy calculations.
2. Engineering and Architecture:
- Structural design: Engineers use square roots in structural calculations to ensure the stability and safety of buildings and bridges.
- Civil Engineering: Determining the lengths and angles of various structural elements frequently involves utilizing square roots.
- Construction: Calculating diagonal measurements and optimizing material usage often requires square root calculations.
3. Finance and Economics:
- Investment calculations: Compound interest calculations involve square roots, used to determine the growth of investments over time.
- Statistical analysis: Standard deviation, a crucial concept in statistics, utilizes square roots in its calculation.
4. Computer Science:
- Graphics and image processing: Square roots are used in various algorithms related to image manipulation, such as scaling and rotation.
- Game development: Calculating distances and speeds within game environments often involves square root computations.
- Cryptography: Some encryption algorithms employ square root operations for security purposes.
5. Everyday Applications:
While not always explicitly calculated, square roots play a role in numerous everyday tasks:
- Estimating distances: Individuals often implicitly use square root concepts when visually estimating distances or paths.
- Cooking and baking: Recipe scaling sometimes involves approximating square roots.
Approximating √512 Without a Calculator
While calculators provide the most convenient way to find the square root of 512, let's explore a practical approximation method. We already know that √512 = 16√2. Since √2 ≈ 1.414, we can multiply 16 by 1.414 to get an approximation: 16 x 1.414 ≈ 22.624. This is close to the value obtained using a calculator.
Conclusion
The square root of 512, while appearing as a simple mathematical problem, reveals the depth and practical relevance of square roots in numerous fields. Understanding different calculation methods, from prime factorization to the Babylonian method, provides a comprehensive grasp of this fundamental concept. Whether using a calculator or employing approximation techniques, the ability to compute square roots is a valuable skill across various disciplines. Remember the approximate value of √512 is 22.627, but understanding the process of deriving this answer is far more important than just knowing the result itself. The journey through the calculations enhances your mathematical understanding and opens doors to numerous applications in the real world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 512 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.