What Is The Square Root Of 76
News Co
Mar 30, 2025 · 5 min read
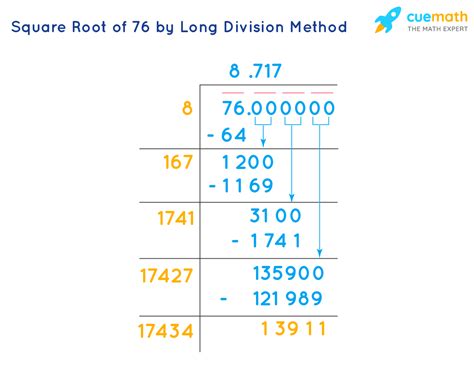
Table of Contents
What is the Square Root of 76? A Deep Dive into Square Roots and Approximation Methods
The question, "What is the square root of 76?" might seem simple at first glance. A quick search on a calculator will give you a decimal approximation. However, exploring this seemingly straightforward question opens up a fascinating world of mathematical concepts, approximation techniques, and the nature of irrational numbers. Let's delve into the intricacies of finding the square root of 76, exploring both precise methods and practical approximations.
Understanding Square Roots
Before we tackle the square root of 76 specifically, let's establish a foundational understanding of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 is 3 because 3 * 3 = 9. This is often represented mathematically as √9 = 3.
Square roots can be categorized into two main types:
- Perfect Squares: These are numbers that have exact integer square roots. Examples include 4 (√4 = 2), 25 (√25 = 5), and 100 (√100 = 10).
- Non-Perfect Squares: These are numbers whose square roots are not integers. They result in irrational numbers, which have decimal representations that continue infinitely without repeating. 76 falls into this category.
Calculating the Square Root of 76: The Precise Approach
Unfortunately, there isn't a neat, whole-number answer to the square root of 76. It's an irrational number. To find a precise value, we can use advanced mathematical techniques, such as the Babylonian method (also known as Heron's method) or Newton-Raphson method. These iterative methods refine an initial guess to progressively closer approximations of the true value.
Let's briefly outline the Babylonian method:
-
Make an initial guess: Start with an educated guess close to the square root of 76. Let's say we guess 8 (because 8 * 8 = 64, which is close to 76).
-
Iterate: The core of the Babylonian method is the iterative formula:
x_(n+1) = 0.5 * (x_n + (N / x_n)), where:x_nis the current guess.x_(n+1)is the next, improved guess.Nis the number whose square root we are seeking (76 in this case).
-
Repeat: We repeat step 2, using the improved guess from the previous iteration as the new
x_n, until the difference between successive guesses becomes negligible (within a desired level of accuracy).
While this method converges to the true value, it's computationally intensive to perform manually for many iterations. Calculators and computer software utilize such algorithms to swiftly determine the square root to a high degree of accuracy.
Approximating the Square Root of 76: Practical Methods
For most practical purposes, a close approximation is sufficient. Here are some methods to approximate the square root of 76 without advanced calculators or complex algorithms:
-
Using a Calculator: The simplest method is to use a calculator or computer software that has a square root function. This will provide a decimal approximation like 8.71779777...
-
Linear Interpolation: Since we know that 8² = 64 and 9² = 81, we can use linear interpolation to estimate the square root of 76. 76 is closer to 81 than to 64, so the square root will be closer to 9 than to 8. A rough estimate would be around 8.7 or 8.8.
-
Babylonian Method (Simplified): Even a few iterations of the Babylonian method yield a reasonable approximation. Let's illustrate:
- Iteration 1:
x_1 = 0.5 * (8 + (76 / 8)) = 8.75 - Iteration 2:
x_2 = 0.5 * (8.75 + (76 / 8.75)) ≈ 8.7179
- Iteration 1:
As you can see, even with just a couple of iterations, we get a fairly accurate approximation.
The Nature of Irrational Numbers: Why 76 Doesn't Have a Neat Answer
The square root of 76 is an irrational number. This means it cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation goes on forever without repeating. This is a fundamental characteristic of many square roots of non-perfect squares. The inability to represent it precisely with a finite number of digits is why we rely on approximations.
Applications of Square Roots
Understanding square roots isn't just an academic exercise. They have numerous practical applications across various fields:
-
Physics: Calculating velocities, distances, and energies often involve square roots.
-
Engineering: Designing structures, analyzing forces, and working with geometrical shapes frequently necessitates the use of square roots.
-
Computer Graphics: Rendering images and animations often utilizes square root calculations for tasks like distance calculations and vector normalization.
-
Finance: Financial models may employ square roots in calculations related to portfolio optimization and risk management.
-
Statistics: Standard deviation and variance calculations heavily rely on square roots.
Conclusion: Embrace the Approximation
While a precise, non-approximate value of the square root of 76 is impossible to obtain and represent, this shouldn't diminish the importance of understanding square roots. The quest to find the square root of 76 leads us through various mathematical concepts and practical approximation techniques. Whether you're using a calculator for quick results or employing iterative methods for greater accuracy, the understanding of the process itself provides valuable insight into the nature of numbers and the power of mathematical tools. Remember, the appropriate method for calculating the square root depends entirely on the level of precision required for your specific application. For everyday purposes, a close approximation is often perfectly adequate. For scientific and engineering applications where higher precision is crucial, more advanced methods become necessary. Regardless of the approach, the journey into the world of square roots reveals a fascinating aspect of mathematics and its importance in our daily lives.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 76 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.