What Is The Square Root Of 86
News Co
Apr 04, 2025 · 5 min read
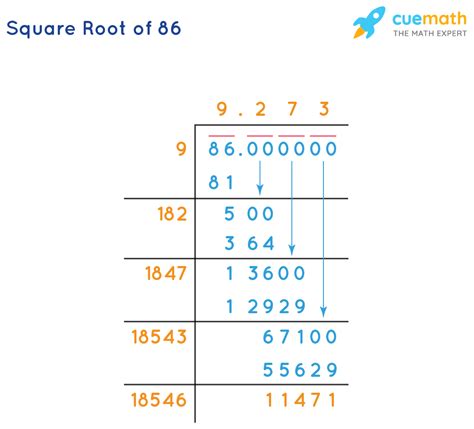
Table of Contents
Decoding the Square Root of 86: A Deep Dive into Irrational Numbers and Approximation Techniques
The seemingly simple question, "What is the square root of 86?" opens a fascinating door into the world of mathematics, specifically the realm of irrational numbers and numerical approximation methods. While a precise, finite decimal representation of √86 is impossible, we can explore several approaches to understanding and calculating its value with increasing accuracy. This article will delve into the theoretical underpinnings, practical calculation methods, and the broader mathematical significance of this seemingly straightforward problem.
Understanding Square Roots and Irrational Numbers
Before we embark on calculating √86, let's establish a firm understanding of the fundamental concepts involved. A square root of a number x is a value that, when multiplied by itself, equals x. In simpler terms, it's the number that, when squared, yields the original number. For example, the square root of 9 (√9) is 3, because 3 × 3 = 9.
However, not all numbers have neat, whole-number square roots. Numbers like 86 fall into the category of irrational numbers. Irrational numbers cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representations are non-terminating and non-repeating – they continue infinitely without ever settling into a repeating pattern. This means we can only approximate the value of √86, getting closer and closer to the true value but never reaching it exactly.
Methods for Approximating √86
Several methods exist for approximating the square root of 86. Let's explore some of the most common and effective techniques:
1. The Babylonian Method (or Heron's Method)
This iterative method refines an initial guess to progressively approach the true square root. The formula is:
x_(n+1) = 0.5 * (x_n + (N / x_n))
where:
x_nis the current approximationx_(n+1)is the next, improved approximationNis the number for which we're finding the square root (in our case, 86)
Let's demonstrate with an initial guess of 9:
- Iteration 1:
x_1 = 0.5 * (9 + (86 / 9)) ≈ 9.2778 - Iteration 2:
x_2 = 0.5 * (9.2778 + (86 / 9.2778)) ≈ 9.2736 - Iteration 3:
x_3 = 0.5 * (9.2736 + (86 / 9.2736)) ≈ 9.2736
As you can see, the method converges rapidly. After just a few iterations, we achieve a high degree of accuracy. The Babylonian method is remarkably efficient and serves as a cornerstone of many numerical algorithms.
2. Using a Calculator or Computer Software
Modern calculators and computer software packages readily provide approximations of square roots. These tools utilize sophisticated algorithms, often variations of the Babylonian method or other advanced techniques, to calculate the square root to a high degree of precision. Using a calculator, we find that √86 is approximately 9.2736184955.
3. Linear Interpolation
This method involves estimating the square root based on known perfect squares. Since 86 lies between 81 (9²) and 100 (10²), we can linearly interpolate:
- The difference between 100 and 81 is 19.
- 86 is 5 units above 81 (86 - 81 = 5).
- The proportion is 5/19.
- We add this proportion of the difference between 9 and 10 (which is 1) to 9: 9 + (5/19) ≈ 9.26
This method provides a rough estimate, but its accuracy is limited compared to the Babylonian method or calculator-based approaches.
4. Newton-Raphson Method
This powerful iterative method, a generalization of the Babylonian method, is widely used in numerical analysis. It involves finding the root of a function, in this case, f(x) = x² - 86. The iterative formula is:
x_(n+1) = x_n - f(x_n) / f'(x_n)
where:
f(x_n)is the value of the function at the current approximation.f'(x_n)is the derivative of the function at the current approximation. In this case, f'(x) = 2x.
The Newton-Raphson method typically converges even faster than the Babylonian method for well-behaved functions.
The Significance of Irrational Numbers
The fact that √86 is irrational highlights a crucial aspect of the number system. While we often encounter whole numbers and fractions in everyday life, the vast majority of numbers are irrational. These numbers, with their infinite and non-repeating decimal expansions, reveal the richness and complexity of the mathematical landscape. Irrational numbers are essential in various fields, including geometry (e.g., the diagonal of a square with side length 1 is √2, an irrational number), calculus, and advanced mathematical modeling.
Practical Applications and Further Exploration
Understanding square roots and approximation techniques has numerous practical applications:
- Engineering and Physics: Calculating distances, areas, and volumes often involve square roots.
- Computer Graphics: Rendering and animation rely on sophisticated mathematical calculations, including square root operations.
- Financial Modeling: Certain financial calculations utilize square roots for risk assessment and portfolio optimization.
- Statistics: Standard deviation calculations frequently require computing square roots.
This exploration of √86 provides a glimpse into a broader mathematical concept. Exploring further into the world of irrational numbers, approximation techniques, and their applications in various fields can lead to a deeper understanding and appreciation of mathematics' profound elegance and power. We've touched upon several methods, each with its own strengths and weaknesses, demonstrating the rich tapestry of numerical analysis. From the simplicity of linear interpolation to the efficiency of the Babylonian and Newton-Raphson methods, there are numerous paths to approximating the seemingly elusive value of √86. Further exploration into these methods, along with the broader field of numerical analysis, will provide a more robust understanding of this fundamental mathematical concept. The seemingly simple question of "What is the square root of 86?" has, in fact, opened a window into a world of fascinating mathematical concepts and applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 86 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.