What Is The Square Root Of 93
News Co
Apr 07, 2025 · 4 min read
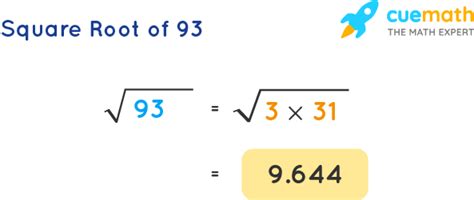
Table of Contents
What is the Square Root of 93? A Deep Dive into Square Roots and Approximation Techniques
The question, "What is the square root of 93?" seems simple at first glance. However, exploring this seemingly straightforward query opens up a fascinating world of mathematical concepts, approximation techniques, and the practical applications of understanding square roots. This article will delve into the intricacies of finding the square root of 93, examining both the theoretical underpinnings and the practical methods used to obtain its value.
Understanding Square Roots
Before we tackle the square root of 93 specifically, let's solidify our understanding of the fundamental concept of a square root. The square root of a number, x, is a value that, when multiplied by itself, equals x. In other words, if √x = y, then y * y = x. This is also represented as y² = x.
For perfect squares (numbers that are the product of an integer multiplied by itself), finding the square root is straightforward. For example, the square root of 16 (√16) is 4 because 4 * 4 = 16. However, 93 is not a perfect square. This means its square root is an irrational number – a number that cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating.
Methods for Approximating √93
Since 93 isn't a perfect square, we need to employ approximation techniques to find its square root. Several methods exist, each with varying degrees of accuracy and complexity:
1. Using a Calculator: The Simplest Approach
The most straightforward method is to use a calculator. Simply input "√93" and the calculator will provide a decimal approximation. Most calculators will give a result around 9.64365076. This is a quick and accurate solution for most practical purposes. However, understanding the underlying methods is crucial for a deeper comprehension of mathematics.
2. The Babylonian Method (or Heron's Method): An Iterative Approach
The Babylonian method is an iterative algorithm that refines an initial guess to progressively approach the true square root. The formula is:
x<sub>n+1</sub> = ½ (x<sub>n</sub> + a/x<sub>n</sub>)
where:
- x<sub>n</sub> is the current approximation
- a is the number whose square root we're seeking (in our case, 93)
- x<sub>n+1</sub> is the next, improved approximation
Let's demonstrate this with an initial guess of 10:
- Iteration 1: x<sub>1</sub> = ½ (10 + 93/10) = 9.65
- Iteration 2: x<sub>2</sub> = ½ (9.65 + 93/9.65) ≈ 9.64365
- Iteration 3: x<sub>3</sub> = ½ (9.64365 + 93/9.64365) ≈ 9.64365076
As you can see, the method converges quickly to the accurate value. Each iteration refines the approximation, providing increased precision.
3. Linear Interpolation: A Simpler Approximation
This method uses the known square roots of perfect squares near 93. We know that √81 = 9 and √100 = 10. Since 93 is between 81 and 100, its square root lies between 9 and 10. We can use linear interpolation to estimate:
Difference between squares: 100 - 81 = 19 Difference between our number and the lower square: 93 - 81 = 12 Proportion: 12/19 ≈ 0.63
Therefore, our approximation is: 9 + 0.63 = 9.63
This method is less precise than the Babylonian method but offers a quick, rough estimation without complex calculations.
4. Using the Binomial Theorem (for advanced users): A More Complex Approach
For those with a stronger mathematical background, the binomial theorem can be used to approximate the square root. This involves expressing √93 as √(100 - 7) and using the binomial series expansion. This method is significantly more complex and requires a deeper understanding of calculus and series expansions.
Practical Applications of Square Roots
Understanding square roots isn't just an academic exercise. They have numerous applications in various fields:
-
Physics: Calculating velocities, distances, and accelerations often involves square roots. For example, the Pythagorean theorem (a² + b² = c²) is fundamental in physics and uses square roots.
-
Engineering: Square roots are essential in structural calculations, determining the strength of materials, and designing various engineering systems.
-
Geometry: Finding the diagonal of a square or rectangle, calculating the area of a circle from its radius all involve square roots.
-
Computer Graphics: Square roots are extensively used in graphics programming for operations such as vector normalization and calculating distances between points.
-
Finance: Calculations related to compound interest and standard deviation in financial modeling often involve square roots.
Conclusion: The Value and Significance of Understanding √93
While a calculator provides the immediate answer (approximately 9.64365), understanding the methods used to arrive at this answer is far more valuable. Exploring different approximation techniques, such as the Babylonian method or linear interpolation, provides insights into fundamental mathematical principles and their practical applications. The journey of approximating √93 is not just about finding a numerical value; it's about understanding the underlying concepts and appreciating the power of mathematical tools. This deeper understanding enhances problem-solving skills and opens doors to a more profound appreciation of mathematics in its various applications. Remember, the pursuit of knowledge, even in something as seemingly simple as finding the square root of 93, is a rewarding endeavor.
Latest Posts
Latest Posts
-
A Quadrilateral With Four Right Angles
Apr 07, 2025
-
Lowest Common Multiple Of 2 And 6
Apr 07, 2025
-
How To Find A Perimeter Of A Rhombus
Apr 07, 2025
-
Prove The Alternate Exterior Angles Theorem
Apr 07, 2025
-
What Is 5 To The 0 Power
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 93 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.