What Is The Square Root Pi
News Co
Apr 06, 2025 · 6 min read
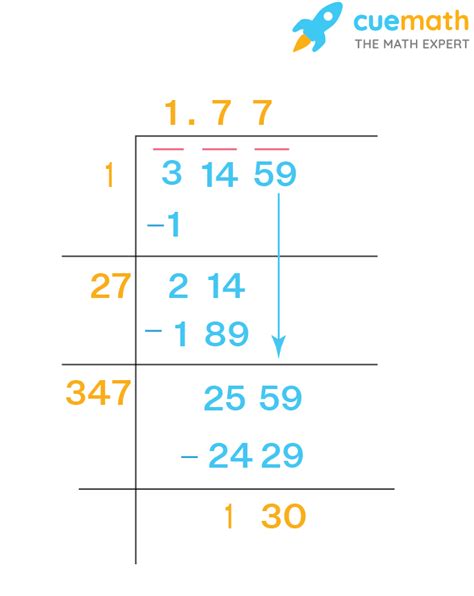
Table of Contents
What is the Square Root of Pi? Unraveling the Mathematical Mystery
The square root of pi (π), denoted as √π, is a fascinating mathematical constant that arises in various fields, from probability and statistics to physics and engineering. While pi itself is widely recognized for its role in circles and spheres, its square root holds a unique significance and deserves exploration. This article delves into the nature of √π, exploring its approximate value, its applications, and its intriguing connection to other mathematical concepts. We'll also touch upon how to calculate it and its significance in various fields.
Understanding Pi (π)
Before we dive into the square root of pi, let's briefly revisit the concept of pi itself. Pi is an irrational number, meaning it cannot be expressed as a simple fraction. It's also a transcendental number, meaning it's not a root of any non-zero polynomial with rational coefficients. Pi is approximately 3.14159, but its decimal representation continues infinitely without repeating.
Pi is defined as the ratio of a circle's circumference to its diameter. This fundamental relationship makes pi essential in geometry and trigonometry, playing a pivotal role in calculating areas, volumes, and other properties of circular and spherical objects.
Calculating the Square Root of Pi (√π)
Since pi is an irrational number, its square root is also irrational. This means we can only approximate its value, not express it exactly. The approximate value of √π is about 1.77245385091.
Several methods can be used to calculate an approximation of √π:
1. Using a Calculator or Computer Software:
The simplest way is to use a calculator or computer software with mathematical functions. Most calculators have a square root function (√), allowing you to directly input π and obtain its square root. More sophisticated software packages, like Mathematica or MATLAB, offer high-precision calculations of √π, providing many more decimal places than a standard calculator.
2. Numerical Methods:
For those interested in the underlying mathematics, numerical methods such as the Newton-Raphson method can be used to approximate the square root. This iterative method refines an initial guess to progressively closer approximations of the square root.
3. Series Expansions:
More advanced mathematical techniques involve using infinite series expansions of √π. These series provide a way to represent √π as an infinite sum of terms, with each successive term contributing to greater accuracy. However, these methods are more complex and require a strong background in calculus.
Applications of √π
The square root of pi, despite being less prominent than pi itself, emerges in a surprising number of applications across diverse fields:
1. Probability and Statistics:
√π appears in various probability distributions, notably the normal distribution. The normal distribution, often referred to as the Gaussian distribution or bell curve, is a fundamental concept in statistics, used to model a wide range of natural phenomena. The standard deviation and variance calculations within the normal distribution involve terms related to √π.
2. Physics and Engineering:
In physics and engineering, √π frequently appears in formulas related to diffusion processes, heat transfer, and wave phenomena. For example, it's found in solutions to the heat equation and the wave equation, both of which describe the temporal evolution of physical quantities such as temperature and wave amplitude.
3. Integration and Calculus:
In integral calculus, √π arises as a result of evaluating certain definite integrals. These integrals often involve Gaussian functions or other functions related to the normal distribution. The presence of √π in these integrals highlights the close relationship between pi, its square root, and the normal distribution.
4. Gamma Function:
The gamma function, a generalization of the factorial function to complex numbers, has a notable connection to √π. Specifically, the gamma function evaluated at 1/2 is equal to √π. This relationship underscores the intricate connection between the gamma function, a powerful tool in mathematical analysis, and the square root of pi.
The Significance of √π in Different Contexts
The significance of √π varies depending on the specific mathematical or scientific context.
1. Normal Distribution:
In statistics, the presence of √π in the formula for the normal distribution's probability density function is crucial. It acts as a normalization constant, ensuring the total probability under the curve integrates to 1, a fundamental requirement for any probability distribution.
2. Probability Density Functions:
√π appears in several other probability density functions besides the normal distribution, for example, the chi-squared distribution and the Student's t-distribution. These distributions are used extensively in statistical inference and hypothesis testing.
3. Error Function:
The error function (erf), a special function used to calculate the probability that a normally distributed random variable falls within a given range, also incorporates √π in its definition. This highlights the close relationship between the error function and the normal distribution, both involving √π.
Mathematical Relationships Involving √π
√π is intrinsically linked to several other mathematical constants and functions.
1. Gamma Function:
As previously mentioned, Γ(1/2) = √π. This identity showcases the profound connection between the square root of pi and the gamma function, a fundamental function in higher mathematics.
2. Gaussian Integral:
The Gaussian integral, ∫_{-∞}^{∞} e^{-x^2} dx = √π, is a famous result in calculus, showcasing a direct relationship between the exponential function and the square root of pi. This integral appears in various physics and engineering applications, especially those dealing with probability distributions.
3. Wallis Product:
The Wallis product formula provides an elegant way to represent pi using an infinite product involving even and odd numbers. While the Wallis product itself doesn't directly involve √π, its close relationship to pi implies an indirect connection to its square root.
Approximations and Numerical Methods
Beyond simple calculator calculations, more sophisticated methods exist for approximating √π to a high degree of precision.
1. Newton-Raphson Method:
The Newton-Raphson method is an iterative technique for finding the roots of a function. It can be applied to find increasingly accurate approximations of √π by repeatedly refining an initial guess.
2. Taylor Series Expansion:
Taylor series expansions provide a way to approximate functions as infinite sums of terms. A Taylor series expansion can be used to represent √(x) around a point, enabling the calculation of √π by substituting the value of π into the series.
Conclusion: The Enduring Significance of √π
The square root of pi, though often overshadowed by its more famous counterpart, pi, holds a significant and nuanced role in mathematics, statistics, physics, and engineering. Its appearance in probability distributions, integral calculus, and the solutions to differential equations highlights its enduring significance across diverse scientific disciplines. Its connection to the gamma function and the Gaussian integral underscores its fundamental importance in advanced mathematics. Further research into its applications and properties will undoubtedly continue to reveal new facets of this fascinating mathematical constant. While its exact value remains elusive, its approximate value and its multifaceted applications remain crucial in various fields, making it a worthy subject of continued exploration and study.
Latest Posts
Latest Posts
-
Are The Diagonals Of A Parallelogram Perpendicular
Apr 07, 2025
-
Place Value Worksheets For 5th Graders
Apr 07, 2025
-
What Are The Common Factors Of 16 And 36
Apr 07, 2025
-
What Is Prime Factorization Of 132
Apr 07, 2025
-
Is 12 Prime Or Composite Number
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
