What Is The Sum 3 X 4 X 2
News Co
Apr 19, 2025 · 5 min read
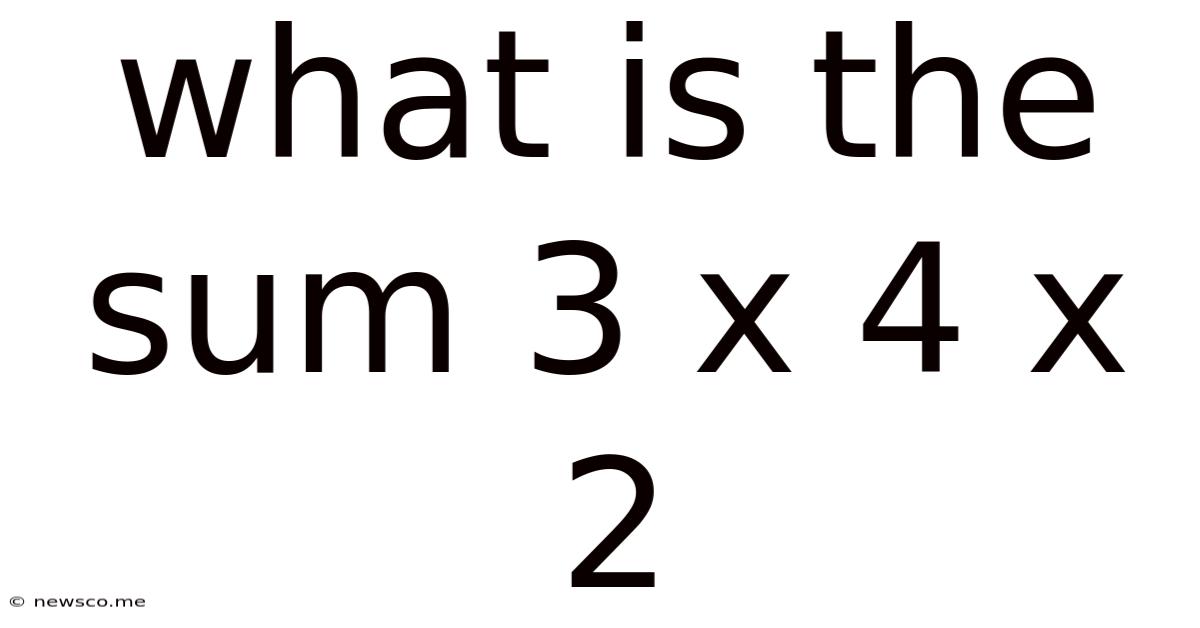
Table of Contents
Decoding the Simple Sum: 3 x 4 x 2 and the Underlying Principles of Multiplication
The seemingly simple equation, 3 x 4 x 2, presents a perfect opportunity to explore fundamental mathematical concepts and delve into the broader world of arithmetic operations. While the answer itself is easily calculable, understanding the why behind the calculation is crucial for developing a robust mathematical foundation. This article will not only solve the equation but will also explore the underlying principles of multiplication, its applications in various fields, and the importance of understanding mathematical processes.
Understanding Multiplication: Beyond Rote Learning
Multiplication, at its core, is repeated addition. When we say 3 x 4, we're essentially saying "add 3 to itself 4 times" (3 + 3 + 3 + 3 = 12). This understanding is crucial, particularly for grasping the concept of multiplication with larger numbers or in more complex equations. It forms the basis for visualizing and comprehending the operation, moving beyond simple memorization of times tables.
The Commutative Property: Order Doesn't Matter (in Multiplication)
One of the fundamental properties of multiplication is the commutative property. This means that the order in which we multiply numbers doesn't affect the final result. For our equation, 3 x 4 x 2 is the same as 4 x 3 x 2, 2 x 3 x 4, and any other permutation of these numbers. This property significantly simplifies calculations and allows for flexibility in solving problems. Understanding this property allows us to choose the most convenient order for multiplication, making complex calculations easier to manage.
The Associative Property: Grouping Numbers for Efficiency
The associative property allows us to group numbers in different ways without altering the final product. We can calculate (3 x 4) x 2 or 3 x (4 x 2). Both groupings will yield the same answer. This is especially useful when dealing with larger numbers or more complex equations. Strategic grouping can simplify the calculation process and reduce the risk of errors. For instance, multiplying 3 x 4 first (giving 12) and then multiplying by 2 (giving 24) is often easier than calculating 4 x 2 first (giving 8) and then multiplying by 3 (giving 24).
Solving the Equation: 3 x 4 x 2
Now, let's solve the equation: 3 x 4 x 2. Using the commutative and associative properties, we can choose the most efficient order of operations.
One approach:
- Multiply 3 x 4: 3 x 4 = 12
- Multiply the result by 2: 12 x 2 = 24
Therefore, the sum of 3 x 4 x 2 is 24.
Another approach, demonstrating the commutative property:
- Multiply 4 x 2: 4 x 2 = 8
- Multiply the result by 3: 8 x 3 = 24
As we can see, regardless of the order of operations, the answer remains the same: 24. This consistency reinforces the fundamental properties of multiplication.
Real-World Applications of Multiplication
Multiplication is not merely an abstract mathematical concept; it's a fundamental operation with widespread applications in various aspects of daily life and specialized fields.
-
Everyday Calculations: Calculating the total cost of multiple items (e.g., buying 3 apples at $4 each), determining the total distance traveled (e.g., driving 2 kilometers four times a day), or finding the area of a rectangular space are all examples of everyday situations that require multiplication.
-
Business and Finance: Multiplication is integral to business calculations, from calculating profits and losses to determining the total revenue generated from selling multiple units of a product. Financial modeling, investment analysis, and budgeting all heavily rely on multiplication.
-
Engineering and Construction: Engineers use multiplication extensively in designing structures, calculating material requirements, and ensuring structural integrity. Calculating the volume of materials needed for a construction project, or the total load-bearing capacity of a bridge are just two examples.
-
Science and Technology: In scientific research and technological advancements, multiplication plays a critical role in data analysis, statistical calculations, and modeling complex systems. From calculating the speed of a moving object to predicting the trajectory of a projectile, multiplication is an essential tool.
-
Computer Science: Multiplication is fundamental to computer programming and algorithms. It is used in performing various computational tasks, from simple arithmetic to complex matrix operations. The speed and efficiency of multiplication algorithms heavily influence the performance of computer systems.
Beyond the Basics: Exploring More Complex Multiplications
While 3 x 4 x 2 is a simple equation, understanding its underlying principles allows us to tackle more complex multiplications with ease. For instance, consider an equation like 15 x 22 x 5. We can apply the same principles of the commutative and associative properties to efficiently solve this:
- Rearrange the numbers: 15 x 5 x 22 (using the commutative property)
- Group numbers for easy multiplication: (15 x 5) x 22
- Calculate the grouped multiplication: 75 x 22
- Perform the final multiplication: 1650
Therefore, 15 x 22 x 5 = 1650.
Conclusion: Mastering the Fundamentals for Future Success
The equation 3 x 4 x 2, although simple in appearance, serves as a gateway to understanding the broader principles of multiplication. By grasping the commutative and associative properties, we can approach even the most complex mathematical problems with efficiency and accuracy. The applications of multiplication extend far beyond the classroom, impacting various aspects of our lives and shaping our understanding of the world around us. Mastering these fundamental concepts provides a solid foundation for tackling more advanced mathematical concepts and problem-solving scenarios. It’s not just about finding the answer (24 in this case); it's about developing a deeper understanding of the process and its significance. This understanding will be invaluable in pursuing further mathematical studies and applying mathematical principles in practical applications. The ability to break down complex problems into simpler, manageable steps is a crucial skill applicable far beyond the realm of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Sum 3 X 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.