What Is The Sum Of 12 5i And 3 4i
News Co
Mar 26, 2025 · 6 min read
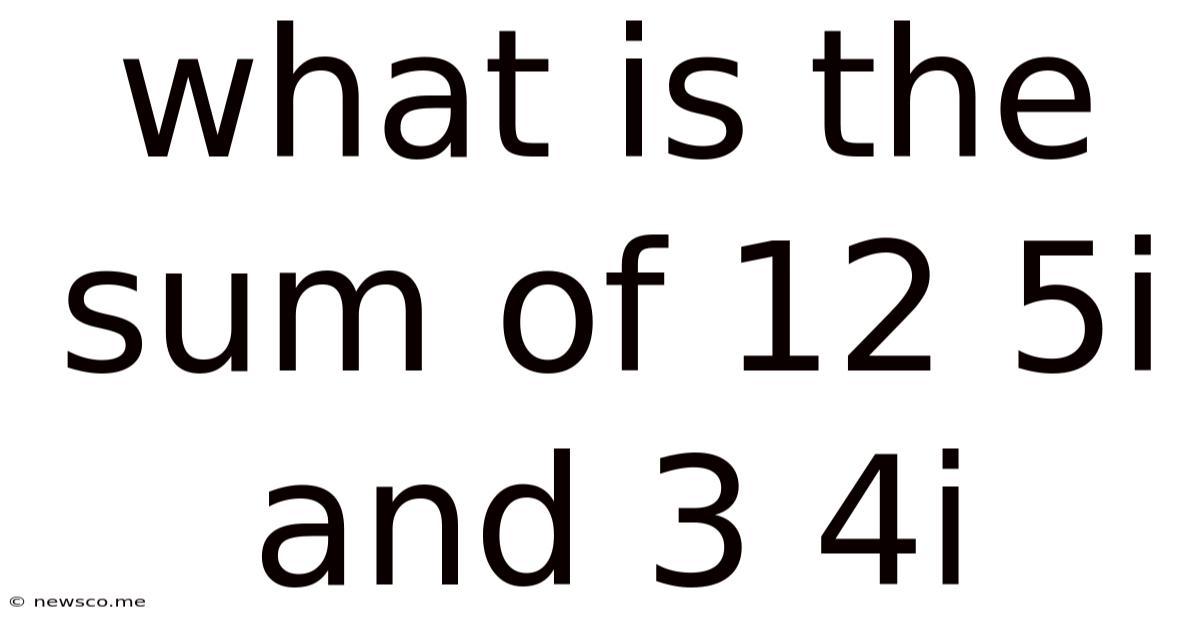
Table of Contents
What is the Sum of 12 + 5i and 3 + 4i? A Deep Dive into Complex Number Addition
This seemingly simple question, "What is the sum of 12 + 5i and 3 + 4i?", opens the door to a fascinating world of complex numbers. While the arithmetic might seem straightforward, understanding the underlying concepts of complex number addition and their representation is crucial for anyone venturing into advanced mathematics, engineering, or physics. This article will not only provide the solution but also delve into the theoretical foundations, practical applications, and various representations of complex numbers.
Understanding Complex Numbers
Before tackling the addition, let's establish a firm grasp on what constitutes a complex number. A complex number is a number that can be expressed in the form a + bi, where:
- a is the real part (a real number).
- b is the imaginary part (a real number).
- i is the imaginary unit, defined as the square root of -1 (√-1).
The set of all complex numbers is denoted by ℂ. Real numbers can be considered a subset of complex numbers where the imaginary part (b) is zero. For example, the number 5 can be written as 5 + 0i.
Visualizing Complex Numbers: The Complex Plane
Complex numbers are not just abstract concepts; they have a beautiful geometric representation. The complex plane (also known as the Argand plane) provides a visual way to understand them. The horizontal axis represents the real part (a), and the vertical axis represents the imaginary part (b). Each complex number can be plotted as a point on this plane, creating a unique visual mapping. This visualization is incredibly helpful in understanding complex number operations like addition and multiplication.
Adding Complex Numbers: A Step-by-Step Guide
Adding complex numbers is remarkably straightforward. It involves adding the real parts separately and the imaginary parts separately. Let's apply this to our problem:
What is the sum of 12 + 5i and 3 + 4i?
-
Identify the real and imaginary parts:
- In 12 + 5i, the real part is 12, and the imaginary part is 5.
- In 3 + 4i, the real part is 3, and the imaginary part is 4.
-
Add the real parts: 12 + 3 = 15
-
Add the imaginary parts: 5 + 4 = 9
-
Combine the results: The sum is 15 + 9i.
Therefore, the sum of 12 + 5i and 3 + 4i is 15 + 9i.
Geometric Interpretation of Complex Number Addition
The addition of complex numbers has a neat geometric interpretation on the complex plane. Imagine plotting each complex number as a vector originating from the origin (0,0). The sum of two complex numbers is represented by the vector obtained by placing the tail of the second vector at the head of the first vector. The resulting vector from the origin to the head of the second vector represents the sum. This is known as vector addition. This visual approach offers a different perspective on the concept, making it more intuitive and easier to grasp.
Other Operations with Complex Numbers
While addition is a fundamental operation, complex numbers support all the standard arithmetic operations:
-
Subtraction: Similar to addition, subtract the real parts and the imaginary parts separately. For instance, (12 + 5i) - (3 + 4i) = (12 - 3) + (5 - 4)i = 9 + i
-
Multiplication: Use the distributive property (FOIL method) and remember that i² = -1. For example, (2 + 3i)(4 + i) = 8 + 2i + 12i + 3i² = 8 + 14i - 3 = 5 + 14i
-
Division: To divide complex numbers, multiply both the numerator and the denominator by the complex conjugate of the denominator. The complex conjugate of a + bi is a - bi. This process eliminates the imaginary part from the denominator.
Applications of Complex Numbers
The seemingly abstract world of complex numbers has surprisingly widespread practical applications across various fields:
-
Electrical Engineering: Complex numbers are fundamental in analyzing alternating current (AC) circuits. They simplify calculations involving impedance, voltage, and current.
-
Signal Processing: Complex numbers are used to represent signals in the frequency domain, enabling efficient signal analysis and manipulation. Techniques like Fourier transforms rely heavily on complex numbers.
-
Quantum Mechanics: The mathematical framework of quantum mechanics heavily utilizes complex numbers to describe the wave function of particles.
-
Fluid Dynamics: Complex analysis is employed to solve complex fluid flow problems.
-
Control Systems: Complex numbers play a vital role in designing and analyzing control systems. Stability analysis often involves complex numbers.
-
Fractals: The generation of fascinating fractal patterns, such as the Mandelbrot set, relies on iterative calculations involving complex numbers.
Different Representations of Complex Numbers
Besides the standard a + bi form, complex numbers can be represented in other ways:
-
Polar Form: This representation uses the magnitude (or modulus) and the argument (or phase) of the complex number. The magnitude, denoted by |z|, represents the distance from the origin to the point representing the complex number in the complex plane. The argument, denoted by θ, represents the angle between the positive real axis and the vector representing the complex number. The polar form is expressed as z = r(cos θ + i sin θ), where r = |z| and θ is the argument. This form is particularly useful in multiplication and division of complex numbers.
-
Exponential Form (Euler's Formula): Euler's formula establishes a remarkable connection between exponential functions and trigonometric functions: e^(iθ) = cos θ + i sin θ. Using this formula, the polar form can be written more compactly as z = re^(iθ). This form is especially convenient for various mathematical operations.
Advanced Concepts and Further Exploration
The world of complex numbers extends far beyond basic addition and subtraction. More advanced topics include:
-
Complex Functions: Functions that map complex numbers to complex numbers. These functions exhibit unique properties and have profound applications in various fields.
-
Cauchy-Riemann Equations: These equations are used to determine whether a complex function is analytic (differentiable) at a given point.
-
Contour Integrals: Integrals evaluated along paths in the complex plane. These integrals have significant applications in solving complex problems.
-
Residue Theorem: A powerful theorem used to evaluate contour integrals. This theorem simplifies the calculation of integrals that would be difficult to solve using traditional methods.
-
Conformal Mapping: A transformation that preserves angles locally. These mappings have applications in solving boundary value problems in physics and engineering.
Conclusion: The Power and Elegance of Complex Numbers
This exploration of complex number addition, while starting with a simple problem, has unveiled the rich tapestry of concepts and applications associated with complex numbers. From their geometric representation on the Argand plane to their diverse applications in various fields, complex numbers demonstrate the power and elegance of mathematics. Understanding complex numbers is not just about performing arithmetic; it's about gaining a deeper appreciation for the mathematical tools that shape our understanding of the world around us. The seemingly simple question, "What is the sum of 12 + 5i and 3 + 4i?", serves as a gateway to a fascinating and rewarding mathematical journey. The answer, 15 + 9i, is just the beginning.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Sum Of 12 5i And 3 4i . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.