What Is The Sum Of Interior Angles Of A Hexagon
News Co
Apr 05, 2025 · 5 min read
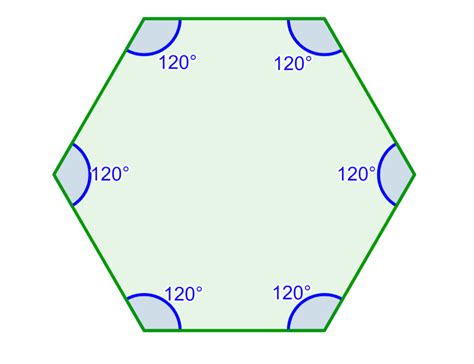
Table of Contents
What is the Sum of Interior Angles of a Hexagon? A Deep Dive into Geometry
The humble hexagon, a six-sided polygon, holds a fascinating secret within its geometric structure: the sum of its interior angles. Understanding this sum isn't just about memorizing a formula; it's about grasping fundamental geometric principles that apply to all polygons, regardless of their number of sides. This article will delve into the various ways to determine the sum of interior angles of a hexagon, exploring different approaches and connecting them to broader mathematical concepts. We'll also touch upon related ideas like exterior angles and the implications for irregular hexagons.
Understanding Polygons and Interior Angles
Before we dive into the specifics of hexagons, let's establish a foundational understanding of polygons and their interior angles. A polygon is a closed two-dimensional figure formed by connecting straight line segments. These segments are called sides, and the points where they meet are called vertices. The interior angles of a polygon are the angles formed inside the polygon at each vertex.
The number of sides of a polygon dictates many of its properties, including the sum of its interior angles. For example:
- Triangle (3 sides): The sum of interior angles is always 180°.
- Quadrilateral (4 sides): The sum of interior angles is always 360°.
- Pentagon (5 sides): The sum of interior angles is always 540°.
Do you see a pattern emerging? As the number of sides increases, so does the sum of the interior angles. This leads us to a general formula, which we'll explore in the next section.
Calculating the Sum of Interior Angles: The Formula
The sum of the interior angles of any polygon can be calculated using a simple formula:
Sum = (n - 2) × 180°
Where 'n' represents the number of sides of the polygon.
Let's apply this to a hexagon:
A hexagon has six sides (n = 6). Substituting this into the formula, we get:
Sum = (6 - 2) × 180° = 4 × 180° = 720°
Therefore, the sum of the interior angles of any hexagon is 720°. This holds true regardless of whether the hexagon is regular (all sides and angles are equal) or irregular (sides and angles are of different lengths and measures).
Triangulation: A Visual Proof
The formula above is powerful, but it can be helpful to visualize why it works. This can be achieved through a technique called triangulation.
Imagine dividing a hexagon into triangles by drawing diagonals from a single vertex to all other non-adjacent vertices. You'll find you can always divide any polygon into (n-2) triangles. Since the sum of angles in a triangle is always 180°, and you have (n-2) triangles, the total sum of interior angles is (n-2) × 180°.
This visualization provides a geometric proof for the formula, making the mathematical concept more intuitive and less abstract. Try this with different polygons – a quadrilateral will form two triangles, a pentagon three, and so on. This method strengthens understanding beyond simply applying the formula.
Regular vs. Irregular Hexagons: A Crucial Distinction
While the sum of interior angles remains constant (720°) for all hexagons, the measure of each individual interior angle varies depending on whether the hexagon is regular or irregular.
-
Regular Hexagon: In a regular hexagon, all sides are equal in length, and all angles are equal in measure. Therefore, each interior angle of a regular hexagon measures 720°/6 = 120°.
-
Irregular Hexagon: In an irregular hexagon, the sides and angles are of varying lengths and measures. While the sum of the interior angles remains 720°, the individual angles can take on a wide range of values, as long as their sum equals 720°.
Exterior Angles: A Complementary Perspective
The exterior angles of a polygon are the angles formed by extending one side of the polygon at each vertex. There's a fascinating relationship between interior and exterior angles. For any polygon, the sum of its exterior angles always equals 360°. This is independent of the number of sides.
This property provides another way to indirectly verify the sum of interior angles for a hexagon. Since the sum of an interior and its corresponding exterior angle is 180°, for a hexagon, the sum of the six pairs would be 6 × 180° = 1080°. Subtracting the sum of exterior angles (360°) from this total gives us the sum of interior angles: 1080° - 360° = 720°.
Applications and Real-World Examples
Understanding the sum of interior angles of a hexagon has practical applications across various fields:
-
Architecture and Engineering: Hexagonal structures are common in architecture and engineering (honeycombs, geodesic domes), and knowing the angle properties is crucial for structural integrity and design.
-
Computer Graphics and Game Development: Hexagonal grids are used in many games and computer graphics for efficient map representations and pathfinding algorithms. Understanding the angles is essential for accurate tile placement and calculations.
-
Crystallography: Many crystals exhibit hexagonal structures. Knowledge of angles helps in analyzing crystal lattice structures and predicting properties.
Beyond Hexagons: Extending the Concept
The principles discussed here extend beyond hexagons to all polygons. The formula (n-2) × 180° for the sum of interior angles applies universally, and the concept of triangulation remains a powerful visualization tool. Understanding these fundamental geometric concepts allows for a deeper appreciation of the elegant relationships within geometric shapes.
Conclusion: Mastering Hexagonal Geometry
Determining the sum of interior angles of a hexagon is more than just applying a formula; it's about understanding the underlying geometric principles that govern polygons. This article explored various approaches to calculating the sum, highlighted the distinction between regular and irregular hexagons, and touched upon the relationship with exterior angles. The applications of this knowledge extend beyond theoretical geometry into practical fields like architecture, engineering, and computer graphics. Mastering this concept forms a strong foundation for further exploration in geometry and related mathematical disciplines. Remember the key takeaway: the sum of interior angles of a hexagon is always 720°, a fundamental truth in the world of shapes and angles.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Sum Of Interior Angles Of A Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.