What Is The Sum Of The Angles In A Hexagon
News Co
Apr 07, 2025 · 6 min read
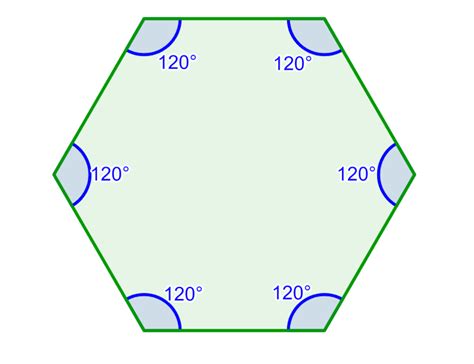
Table of Contents
What is the Sum of the Angles in a Hexagon? A Comprehensive Guide
Understanding the sum of interior angles in a polygon, particularly a hexagon, is fundamental in geometry. This comprehensive guide will delve into the calculation, explore different approaches, and demonstrate its applications in various fields. We'll also touch upon related concepts to solidify your understanding.
What is a Hexagon?
A hexagon is a polygon with six sides and six angles. Polygons are two-dimensional closed shapes formed by straight lines. Hexagons come in various forms, each with unique properties:
- Regular Hexagon: All sides and angles are equal. Each interior angle measures 120 degrees.
- Irregular Hexagon: Sides and angles are of different lengths and measures. The sum of interior angles remains consistent, irrespective of its regularity.
Calculating the Sum of Interior Angles in a Hexagon
There are several ways to determine the sum of interior angles in a hexagon. Let's explore the most common and effective methods:
Method 1: Triangulation
This is arguably the most intuitive method. We can divide any hexagon into triangles by drawing diagonals from a single vertex. A hexagon can be divided into four triangles.
Since the sum of angles in a triangle is always 180 degrees, and we have four triangles, the total sum of interior angles in the hexagon is:
4 triangles * 180 degrees/triangle = 720 degrees
Therefore, the sum of interior angles in any hexagon, regardless of its shape, is 720 degrees.
Method 2: Using the Formula
A more generalized approach involves using a formula that works for any polygon, including a hexagon. The formula for the sum of interior angles (S) of an n-sided polygon is:
S = (n - 2) * 180 degrees
Where 'n' represents the number of sides.
For a hexagon (n = 6), the calculation is:
S = (6 - 2) * 180 degrees = 4 * 180 degrees = 720 degrees
This formula elegantly confirms our previous finding, reinforcing the consistency of the sum of interior angles in a hexagon.
Method 3: Exterior Angles
While less intuitive for finding the sum of interior angles, understanding exterior angles provides a valuable alternative perspective. An exterior angle is formed by extending one side of a polygon. The sum of exterior angles in any polygon is always 360 degrees.
Knowing this, we can indirectly determine the interior angle sum. Each interior angle and its corresponding exterior angle are supplementary (add up to 180 degrees). Let's denote an interior angle as 'I' and its corresponding exterior angle as 'E'. Then:
I + E = 180 degrees
In a hexagon, we have six interior and six exterior angles. The sum of exterior angles is 360 degrees. Therefore:
6 * E = 360 degrees E = 60 degrees
Since I + E = 180 degrees, we can solve for the sum of interior angles:
6 * I = 6 * (180 - 60) = 6 * 120 = 720 degrees
This method, though more circuitous, effectively demonstrates the interconnectedness of interior and exterior angles and their relationship to the overall polygon properties.
Applications of Hexagon Angle Sum
The knowledge of the 720-degree sum of interior angles in a hexagon has various practical applications across multiple disciplines:
1. Architecture and Engineering
Hexagonal structures are prevalent in architecture and engineering due to their strength and efficient use of space. Understanding the angle properties is crucial for:
- Structural Integrity: Accurate calculations are essential for ensuring the stability and strength of hexagonal buildings, bridges, or other structures. Improper angles can compromise structural integrity.
- Tessellations: Hexagons, particularly regular hexagons, tessellate perfectly (fit together without gaps) making them ideal for floor tiling, paving, or honeycomb structures. Understanding angles is critical for seamless design.
2. Cartography and Geography
Hexagonal grids are used in geographic information systems (GIS) and cartography for:
- Data Representation: Hexagonal grids offer a more accurate representation of spatial data compared to square grids, especially in areas with irregular features.
- Spatial Analysis: The geometry of hexagons allows for efficient spatial analysis and data interpolation.
3. Computer Graphics and Game Development
Hexagons are frequently used in:
- Tile-based Games: Many strategy and role-playing games utilize hexagonal grids for map representation. Understanding angle properties helps in creating realistic and functional game environments.
- 3D Modeling: Hexagonal shapes are employed in creating complex 3D models for various applications.
4. Nature and Biology
Hexagonal structures appear frequently in nature:
- Honeycomb: Honeybees construct their honeycombs using hexagonal cells, a testament to nature's optimization of space and material use.
- Crystal Structures: Some crystals exhibit hexagonal structures, where understanding angles is crucial for identifying and classifying them.
Beyond the Hexagon: Generalizing to Other Polygons
The principles discussed for hexagons apply to other polygons as well. The formula (n - 2) * 180 degrees provides a universal method for calculating the sum of interior angles for any polygon with 'n' sides.
Solving Problems Related to Hexagon Angles
Let's tackle some example problems to reinforce our understanding:
Problem 1: A regular hexagon has an interior angle of 120 degrees. Verify this using the formula.
Solution: We know the sum of interior angles is 720 degrees. Since it's a regular hexagon, all angles are equal. Therefore, each interior angle is:
720 degrees / 6 sides = 120 degrees
This verifies the known measure of an interior angle in a regular hexagon.
Problem 2: An irregular hexagon has five interior angles measuring 110, 115, 125, 130, and 140 degrees. Find the measure of the sixth angle.
Solution: The sum of all six angles must be 720 degrees. We add the known angles:
110 + 115 + 125 + 130 + 140 = 620 degrees
To find the remaining angle, subtract this sum from the total:
720 degrees - 620 degrees = 100 degrees
The sixth angle measures 100 degrees.
Problem 3: A hexagon is divided into triangles. How many triangles are formed? Explain its relation to the formula.
Solution: A hexagon can be divided into four triangles. This directly relates to the formula (n-2) * 180. The (n-2) represents the number of triangles formed. For a hexagon (n=6), this yields 4 triangles, each contributing 180 degrees to the total sum.
Conclusion
Understanding the sum of angles in a hexagon is not just an academic exercise. It's a fundamental geometric concept with far-reaching applications in diverse fields. By mastering the various methods of calculation and exploring the practical implications, you'll gain a deeper appreciation for the elegance and power of geometry. The formula (n-2) * 180 degrees provides a powerful and versatile tool for solving problems related to polygons of any number of sides, extending beyond just the hexagon. Remember that whether it’s a regular or irregular hexagon, the sum of its interior angles will always be 720 degrees.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Sum Of The Angles In A Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.