What Is The Sum Of The Interior Angles Of Hexagon
News Co
Apr 08, 2025 · 5 min read
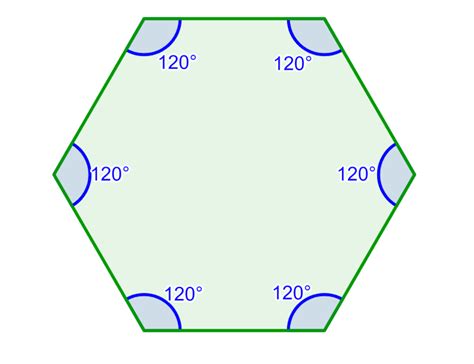
Table of Contents
What is the Sum of the Interior Angles of a Hexagon? A Comprehensive Guide
The humble hexagon, a six-sided polygon, holds a fascinating mathematical property: a consistent sum of its interior angles. Understanding this property is fundamental to geometry, and its applications extend far beyond the classroom, impacting fields like architecture, engineering, and even the study of natural structures like honeycombs. This comprehensive guide will explore the sum of the interior angles of a hexagon, providing different approaches to understanding this concept, and highlighting its practical significance.
Understanding Polygons and Their Angles
Before diving into the specifics of hexagons, let's establish a foundational understanding of polygons. A polygon is a closed, two-dimensional figure formed by connecting three or more line segments. These line segments are called the sides of the polygon. The points where the sides meet are called vertices.
Polygons are classified based on the number of sides they have. Some common examples include:
- Triangle: 3 sides
- Quadrilateral: 4 sides (e.g., square, rectangle, trapezoid)
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon (or Septagon): 7 sides
- Octagon: 8 sides
- Nonagon: 9 sides
- Decagon: 10 sides
and so on.
Each polygon possesses interior angles, which are the angles formed inside the polygon at each vertex. The sum of these interior angles is a crucial characteristic of any polygon.
Calculating the Sum of Interior Angles: The Formula Approach
The sum of the interior angles of any polygon can be calculated using a simple formula. This formula relates the number of sides of the polygon to the sum of its interior angles. The formula is:
(n - 2) * 180°
where 'n' represents the number of sides of the polygon.
Let's apply this formula to a hexagon, where n = 6:
(6 - 2) * 180° = 4 * 180° = 720°
Therefore, the sum of the interior angles of a hexagon is 720°. This holds true for any hexagon, regardless of its shape or size, as long as it is a closed six-sided figure.
Triangulation Method: A Visual Understanding
While the formula provides a quick and efficient way to calculate the sum of interior angles, the triangulation method offers a more intuitive visual understanding. This method involves dividing the polygon into a series of triangles.
Consider a hexagon. We can divide it into four triangles by drawing diagonals from one vertex to the other non-adjacent vertices. Each triangle has an interior angle sum of 180°. Since we have four triangles, the total sum of the interior angles of the hexagon is 4 * 180° = 720°.
This method visually demonstrates why the (n - 2) * 180° formula works. The (n - 2) part represents the number of triangles that can be formed within the polygon.
Regular vs. Irregular Hexagons: A Note on Angle Measures
It's crucial to distinguish between regular and irregular hexagons. A regular hexagon has all sides of equal length and all interior angles of equal measure. In a regular hexagon, each interior angle measures 720°/6 = 120°.
An irregular hexagon, on the other hand, has sides and angles of varying lengths and measures. While the sum of the interior angles remains 720°, the individual angle measures will differ. The specific measures of each angle in an irregular hexagon will depend on the specific dimensions of the hexagon.
Practical Applications of Hexagon Geometry
The properties of hexagons, particularly the sum of their interior angles, find applications in various fields:
Architecture and Engineering:
- Honeycomb structures: The hexagonal shape is prevalent in nature, notably in honeycombs. The efficiency of this structure is directly related to the properties of hexagons, including their ability to tessellate (tile a surface without gaps) and maximize space utilization while minimizing material usage.
- Structural designs: Hexagonal shapes can provide significant structural strength and stability in engineering designs. Their inherent symmetry contributes to balanced load distribution.
- Tile patterns: Hexagonal tiles are frequently used in flooring and wall designs due to their aesthetic appeal and ability to create seamless patterns.
Mathematics and Computer Science:
- Tessellations: Hexagons are one of only three regular polygons that can tessellate a plane completely. This property is significant in various mathematical and computational applications.
- Graph theory: Hexagonal grids are used in graph theory and network analysis to represent relationships and connections.
Other Applications:
- Crystallography: The hexagonal crystal system is a common arrangement of atoms in various materials.
- Game design: Hexagonal grids are used in board games and video games to create unique gameplay mechanics.
Beyond Hexagons: Generalizing to Other Polygons
The principles discussed for hexagons can be generalized to other polygons. The formula (n - 2) * 180° allows us to calculate the sum of interior angles for polygons with any number of sides. For example:
- Pentagon (n=5): (5 - 2) * 180° = 540°
- Heptagon (n=7): (7 - 2) * 180° = 900°
- Octagon (n=8): (8 - 2) * 180° = 1080°
Understanding the relationship between the number of sides and the sum of interior angles is crucial for a deeper understanding of geometry and its practical applications.
Conclusion: The Significance of Hexagon Geometry
The sum of the interior angles of a hexagon, consistently 720°, is a fundamental geometric concept with wide-ranging applications. Whether calculated using the formula or visualized through triangulation, the understanding of this property is essential for students and professionals alike. From the natural world's efficient honeycomb structures to the design of buildings and the development of algorithms, hexagons and their properties continue to impact various fields, solidifying their place as a cornerstone of geometric understanding. The exploration of this simple polygon unveils a surprisingly rich tapestry of mathematical concepts and practical applications. Further investigation into the properties of polygons can lead to a deeper appreciation of the elegance and utility of geometry in the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Sum Of The Interior Angles Of Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.