What Is The Value Of 4 3
News Co
Apr 19, 2025 · 5 min read
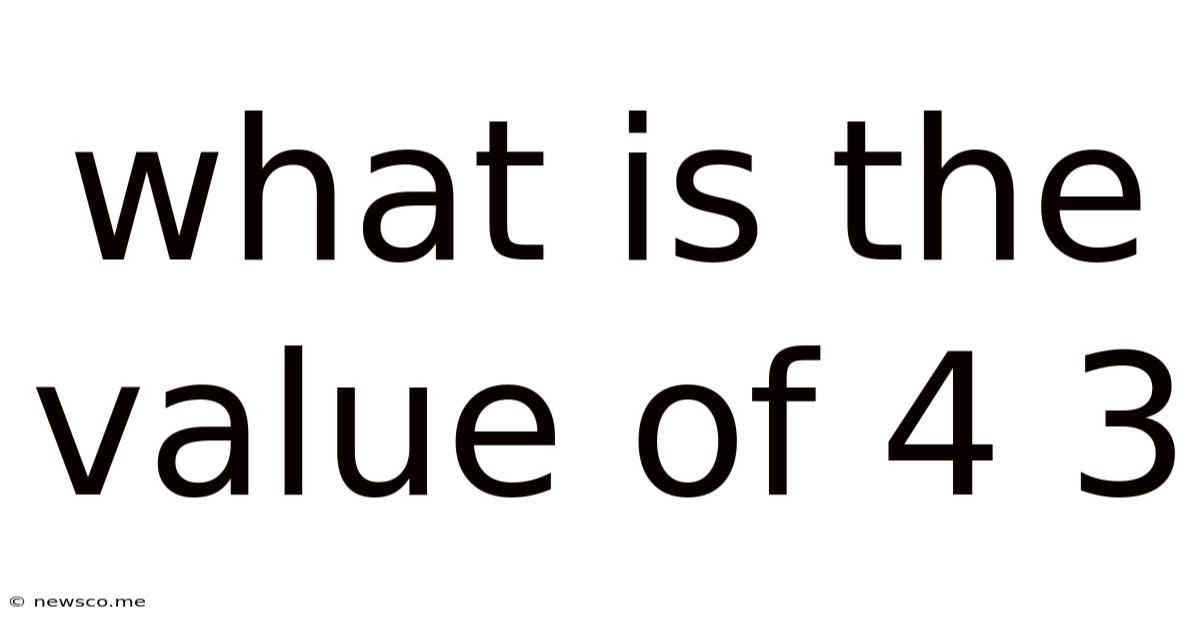
Table of Contents
What is the Value of 4^3? Understanding Exponents and Their Applications
The question, "What is the value of 4^3?", might seem simple at first glance. However, it opens the door to a broader understanding of exponents, their applications in various fields, and the importance of mathematical notation. This article will delve into the answer, exploring the concept of exponentiation, its practical uses, and related mathematical concepts.
Understanding Exponents: The Power of Repeated Multiplication
In mathematics, an exponent (also known as a power or index) represents repeated multiplication. The expression 4^3, read as "4 raised to the power of 3" or "4 cubed," signifies 4 multiplied by itself three times. Therefore:
4^3 = 4 * 4 * 4 = 64
The number 4 is called the base, and the number 3 is the exponent. The exponent indicates how many times the base is multiplied by itself.
Simple Examples to Illustrate the Concept
Let's look at a few more examples to solidify the understanding of exponents:
- 2^2 = 2 * 2 = 4 (2 squared)
- 3^4 = 3 * 3 * 3 * 3 = 81 (3 raised to the power of 4)
- 10^1 = 10 (10 raised to the power of 1 – any number raised to the power of 1 is itself)
- 5^0 = 1 (Any non-zero number raised to the power of 0 is 1. This is a fundamental rule in exponentiation.)
Beyond Simple Calculations: The Significance of Exponents
While calculating 4^3 might seem trivial, the concept of exponentiation has profound implications across numerous fields:
1. Scientific Notation and Very Large or Very Small Numbers
Exponents are essential for representing extremely large or small numbers in a concise manner. Scientific notation uses powers of 10 to express these values. For example, the speed of light is approximately 3 x 10^8 meters per second. This is far more manageable than writing out 300,000,000. Similarly, the size of an atom might be expressed using negative exponents, indicating a very small number.
2. Compound Interest and Financial Growth
Understanding exponents is crucial for comprehending the power of compound interest. Compound interest is interest earned not only on the principal amount but also on accumulated interest. The formula for compound interest involves exponents, demonstrating the exponential growth of investments over time.
3. Exponential Growth and Decay in Nature and Science
Many natural phenomena exhibit exponential growth or decay. Examples include:
- Population growth: Under ideal conditions, populations can grow exponentially.
- Radioactive decay: The rate at which radioactive materials decay follows an exponential pattern.
- Spread of diseases: In the initial stages, the spread of infectious diseases can often be modeled using exponential functions.
4. Computer Science and Algorithms
Exponents play a vital role in computer science. Algorithms' efficiency is often analyzed using Big O notation, which uses exponents to describe the growth rate of an algorithm's time or space complexity. Understanding these growth rates is critical for optimizing software performance.
Exploring Related Mathematical Concepts
The understanding of 4^3 is intrinsically linked to several other mathematical concepts:
1. Roots and Radicals
The inverse operation of exponentiation is finding the root. For example, the cube root of 64 (∛64) is 4 because 4 * 4 * 4 = 64. Roots and exponents are fundamental concepts used in solving equations and simplifying expressions.
2. Logarithms
Logarithms are another essential concept closely related to exponents. The logarithm of a number is the exponent to which another fixed value (the base) must be raised to produce that number. For instance, the base-10 logarithm of 100 is 2 (log₁₀(100) = 2) because 10² = 100. Logarithms are used extensively in various fields, such as chemistry, physics, and engineering, for solving exponential equations and analyzing data.
3. Polynomial Equations
Exponents are a critical component of polynomials. Polynomials are mathematical expressions consisting of variables and coefficients, involving non-negative integer exponents. Solving polynomial equations is a significant aspect of algebra and calculus and has wide-ranging applications in numerous fields.
Practical Applications and Real-World Examples
The understanding and application of exponents extend far beyond theoretical mathematics. Here are some real-world examples:
- Calculating the volume of a cube: If a cube has sides of length 4 units, its volume is 4^3 = 64 cubic units. This highlights the direct relationship between exponents and geometric calculations.
- Understanding bacterial growth: If a bacterial colony doubles in size every hour, its growth can be modeled using an exponential function, showing how quickly the population increases over time.
- Analyzing investment returns: The power of compound interest, as discussed earlier, is directly dependent on exponential calculations, impacting long-term investment strategies.
- Modeling the spread of information: The rate at which news or information spreads across social media or other networks can often be approximated using exponential functions.
Beyond the Basics: More Complex Exponents
While 4^3 is a relatively simple example, the concept of exponents extends to include:
- Fractional exponents: These represent roots, such as 4^(1/2) which is the square root of 4, equal to 2.
- Negative exponents: These represent reciprocals, such as 4^(-1) which is equal to 1/4.
- Decimal exponents: These can represent combinations of roots and powers.
Mastering these more advanced concepts builds a solid foundation for tackling complex mathematical problems and analyzing data in various fields.
Conclusion: The Enduring Importance of 4^3 and Exponentiation
The seemingly simple question, "What is the value of 4^3?", serves as a gateway to a vast and significant area of mathematics – exponentiation. This concept is fundamental to understanding various scientific, financial, and technological phenomena. From calculating compound interest to modeling population growth or analyzing algorithm efficiency, exponents are indispensable tools. By grasping the core concepts and their applications, we can unlock a deeper understanding of the world around us and effectively utilize mathematical principles to solve real-world problems. The value of 4^3 is 64, but the value of understanding exponents extends far beyond this single calculation.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Value Of 4 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.