What Is The Value Of 7 3i 2 6i
News Co
Mar 26, 2025 · 4 min read
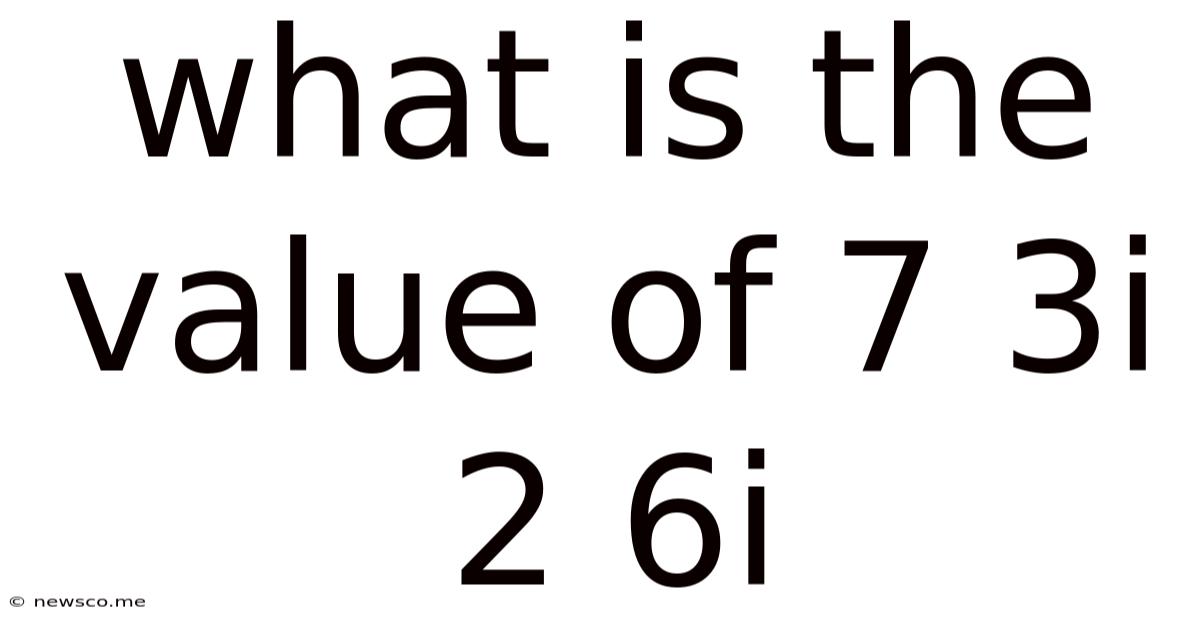
Table of Contents
What is the Value of 7 + 3i + 2 + 6i? A Deep Dive into Complex Numbers
This article explores the seemingly simple question: What is the value of 7 + 3i + 2 + 6i? While the calculation itself is straightforward, it presents a valuable opportunity to delve into the fascinating world of complex numbers, their properties, and their applications. We'll unpack the concept, explain the solution, and then explore the broader significance of complex numbers in mathematics and beyond.
Understanding Complex Numbers
Before we tackle the problem, let's establish a firm understanding of complex numbers. A complex number is a number that can be expressed in the form a + bi, where:
- a is the real part of the complex number.
- b is the imaginary part of the complex number.
- i is the imaginary unit, defined as the square root of -1 (√-1).
The introduction of the imaginary unit, 'i', allows us to solve equations that would otherwise have no solution within the realm of real numbers. For example, the equation x² = -1 has no real solutions, but it has two complex solutions: x = i and x = -i.
Visualizing Complex Numbers: The Complex Plane
Complex numbers can be visualized graphically on the complex plane, also known as the Argand plane. In this plane:
- The horizontal axis represents the real part (a).
- The vertical axis represents the imaginary part (b).
Each complex number can be plotted as a point on this plane, with its coordinates corresponding to its real and imaginary parts. This visual representation helps in understanding the magnitude and direction of complex numbers.
Solving 7 + 3i + 2 + 6i
Now, let's address the question at hand: What is the value of 7 + 3i + 2 + 6i?
The solution involves combining the real parts and the imaginary parts separately:
- Combine the real parts: 7 + 2 = 9
- Combine the imaginary parts: 3i + 6i = 9i
Therefore, the value of 7 + 3i + 2 + 6i is 9 + 9i.
This simple addition highlights a fundamental property of complex numbers: they are added (and subtracted) component-wise.
Operations with Complex Numbers: Beyond Addition
While addition is relatively straightforward, complex numbers allow for a broader range of operations, including:
Subtraction:
Subtracting complex numbers follows a similar principle to addition. We subtract the real parts and the imaginary parts separately. For example:
(a + bi) - (c + di) = (a - c) + (b - d)i
Multiplication:
Multiplication of complex numbers uses the distributive property (FOIL method) and the fact that i² = -1. For example:
(a + bi)(c + di) = ac + adi + bci + bdi² = (ac - bd) + (ad + bc)i
Division:
Dividing complex numbers involves multiplying both the numerator and denominator by the complex conjugate of the denominator. The complex conjugate of a + bi is a - bi. This eliminates the imaginary part from the denominator. For example:
(a + bi) / (c + di) = [(a + bi)(c - di)] / [(c + di)(c - di)] = [(ac + bd) + (bc - ad)i] / (c² + d²)
Applications of Complex Numbers
Complex numbers, despite their seemingly abstract nature, have far-reaching applications in various fields:
Engineering and Physics:
- Electrical Engineering: Complex numbers are crucial for analyzing alternating current (AC) circuits. They simplify calculations involving impedance, voltage, and current.
- Signal Processing: Complex numbers are used extensively in Fourier analysis, which is fundamental to signal processing and image processing.
- Quantum Mechanics: Complex numbers are essential for describing quantum states and wave functions.
- Fluid Dynamics: Complex analysis provides powerful tools for solving problems related to fluid flow.
Mathematics:
- Algebra: Complex numbers extend the field of real numbers, enabling solutions to polynomial equations that are impossible with real numbers alone.
- Calculus: Complex analysis provides powerful techniques for solving differential equations and evaluating integrals.
- Number Theory: Complex numbers play a significant role in advanced number theory, including the study of prime numbers and Diophantine equations.
Other Applications:
- Fractals: Complex numbers are instrumental in generating fractals, such as the Mandelbrot set, which exhibit stunning and intricate patterns.
- Computer Graphics: Complex numbers contribute to techniques like rotations and transformations in computer graphics.
The Significance of Understanding Complex Numbers
The seemingly simple calculation of 7 + 3i + 2 + 6i serves as a gateway to understanding a rich and powerful mathematical concept. Mastering complex numbers opens doors to advanced mathematical concepts and a wide array of practical applications in science and engineering. The ability to manipulate and understand these numbers is an invaluable skill for students and professionals alike.
Conclusion: Beyond the Sum
While the answer to "What is the value of 7 + 3i + 2 + 6i?" is simply 9 + 9i, the true value lies in the broader understanding it provides. This seemingly elementary problem acts as a stepping stone to a world of sophisticated mathematical tools with profound real-world implications. By understanding complex numbers, we gain a deeper appreciation for the elegance and power of mathematics and its capacity to model and solve complex problems across diverse fields. So, while the sum is straightforward, the journey into the realm of complex numbers is an ongoing exploration filled with intellectual reward and practical utility. Remember to practice these operations; the more you work with complex numbers, the more intuitive they become.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of 7 3i 2 6i . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.