What Is The Value Of X 14 15 16 17
News Co
Apr 08, 2025 · 6 min read
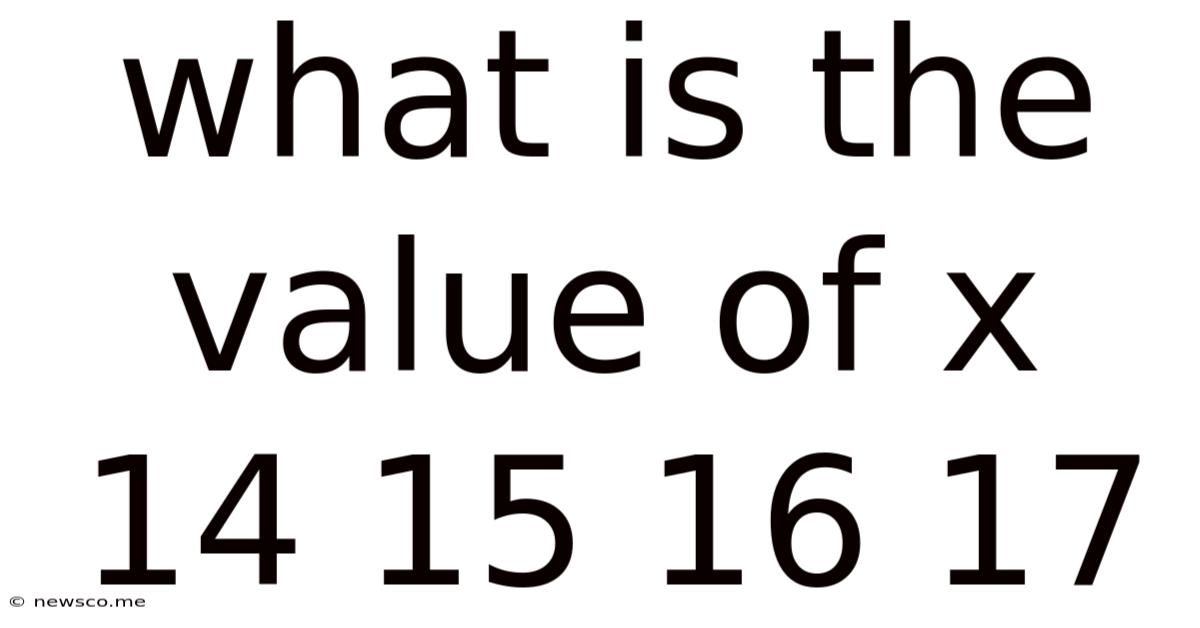
Table of Contents
Decoding the Mystery: What is the Value of x in the Sequence 14, 15, 16, 17? A Deep Dive into Mathematical Reasoning
The seemingly simple question, "What is the value of x in the sequence 14, 15, 16, 17?" might initially appear trivial. However, a closer examination reveals a fascinating exploration into mathematical reasoning, the importance of context, and the diverse approaches to problem-solving. This seemingly straightforward numerical sequence offers a rich platform to discuss various mathematical concepts, from simple arithmetic progression to more complex pattern recognition techniques.
Understanding the Obvious: Arithmetic Progression
At first glance, the sequence 14, 15, 16, 17 immediately suggests an arithmetic progression. An arithmetic progression (or arithmetic sequence) is a sequence of numbers such that the difference between any two consecutive terms is constant. This constant difference is known as the common difference.
In our sequence, the common difference is clearly 1:
- 15 - 14 = 1
- 16 - 15 = 1
- 17 - 16 = 1
Therefore, if x represents the next term in the sequence, logically, x = 17 + 1 = 18. This is the most straightforward and immediate answer. The value of x, based on a simple arithmetic progression, is undeniably 18.
Beyond the Obvious: Exploring Potential Ambiguity
While the arithmetic progression provides a clear and concise solution, it's crucial to acknowledge the potential for ambiguity in mathematical problems. The question itself is intentionally open-ended, lacking explicit constraints or a defined context. This lack of context allows for more creative and nuanced interpretations.
For example, what if the sequence isn't a simple arithmetic progression? What if the numbers represent something else entirely? This opens the door to considering more complex mathematical concepts and alternative interpretations.
The Importance of Context: Reframing the Problem
The value of x hinges heavily on the context in which the sequence is presented. Consider these alternative scenarios:
-
Scenario 1: A Code or Cipher: The sequence 14, 15, 16, 17 could represent a coded message or a part of a larger cipher. In this case, the value of x wouldn't simply be the next number in a numerical progression. It would depend on the specific code or cipher being used. Further information would be needed to decipher the code and determine x's value. For example, it could be a Caesar cipher with a shift of 1, or an even more complex substitution cipher.
-
Scenario 2: Experimental Data: The numbers could represent experimental data points, perhaps measurements taken at regular intervals. In this context, x wouldn't necessarily follow a perfectly predictable pattern. Factors like experimental error or external influences could affect the next measurement. Statistical analysis would be necessary to predict the next value. Techniques like linear regression could be employed to fit a line of best fit to the data and estimate the value of x based on the trend.
-
Scenario 3: A Subset of a Larger Sequence: The provided sequence might be a small segment of a much larger, more intricate sequence. Without the full context, it's impossible to definitively determine the value of x. The larger sequence might follow a recursive pattern, a Fibonacci-like sequence, or some other complex mathematical relationship. Analysis of a larger dataset is crucial for uncovering hidden patterns.
Expanding the Scope: Introducing More Complex Mathematical Concepts
Let's explore how different mathematical concepts might influence our understanding of this sequence and the determination of x:
-
Polynomial Sequences: The sequence could be a subset of a polynomial sequence. For instance, a quadratic sequence could generate these numbers as part of its larger pattern. This would require applying techniques to determine the coefficients of the polynomial that generates the given values. Fitting a polynomial curve to the data would allow us to extrapolate and find the next value of x.
-
Recurrence Relations: The sequence might be defined by a recurrence relation – a formula that expresses each term as a function of the preceding terms. Finding the appropriate recurrence relation would require careful analysis and mathematical intuition.
-
Modular Arithmetic: The numbers could be considered modulo some integer. For instance, if we consider the sequence modulo 10, the values wouldn't change significantly, but a different modulo could dramatically alter the pattern and the value of x.
-
Geometric Progressions: Though less likely given the presented sequence, it's worth noting that geometric progressions exist where each term is multiplied by a constant to obtain the next. This is clearly not the case here, but its inclusion highlights the breadth of mathematical possibilities.
The Role of Pattern Recognition and Deductive Reasoning
The core of solving this type of problem lies in pattern recognition and deductive reasoning. While the arithmetic progression offers the simplest explanation, it's vital to consider that more complex patterns might exist, hidden beneath the surface of these four seemingly simple numbers. Effective problem-solving involves systematically considering various possibilities and using available information to eliminate improbable scenarios.
This exercise underlines the importance of critically analyzing a problem's context and embracing the possibility of multiple valid solutions, depending on the assumptions made and the information available. The seemingly simple sequence 14, 15, 16, 17 becomes a microcosm of the broader mathematical landscape, demonstrating the power of different analytical approaches and the limitations of incomplete information.
Practical Applications and Real-World Examples
The process of analyzing numerical sequences and predicting future values has numerous applications across diverse fields:
-
Data Science and Machine Learning: Predicting future trends in stock prices, weather patterns, or consumer behavior often involves analyzing historical data sequences and applying sophisticated mathematical models to forecast future values.
-
Financial Modeling: Financial analysts rely heavily on sequence analysis to predict economic indicators, assess investment risks, and make informed decisions about financial strategies.
-
Engineering and Physics: Many physical phenomena are described by sequences or series. Analyzing these sequences is essential for understanding the underlying principles and predicting the behavior of systems.
-
Cryptography: The analysis of numerical sequences forms the basis of various cryptographic techniques, used to encrypt and decrypt sensitive information.
Conclusion: The Value of X and the Value of Exploration
The seemingly simple question of "What is the value of x?" in the sequence 14, 15, 16, 17 serves as a powerful reminder of the depth and complexity inherent in even the most elementary mathematical concepts. While the most straightforward answer, x = 18, based on an arithmetic progression, is certainly a valid solution, the exercise encourages us to think critically, explore alternative possibilities, and embrace the multifaceted nature of mathematical reasoning. The true value lies not just in finding the answer but in the journey of exploration and the development of analytical skills that can be applied across a wide range of disciplines. The problem highlights the importance of context, the power of pattern recognition, and the boundless potential of mathematical thinking. It's a testament to the beauty and utility of mathematics in our world.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Value Of X 14 15 16 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.