What Is X Squared Minus X
News Co
May 03, 2025 · 6 min read
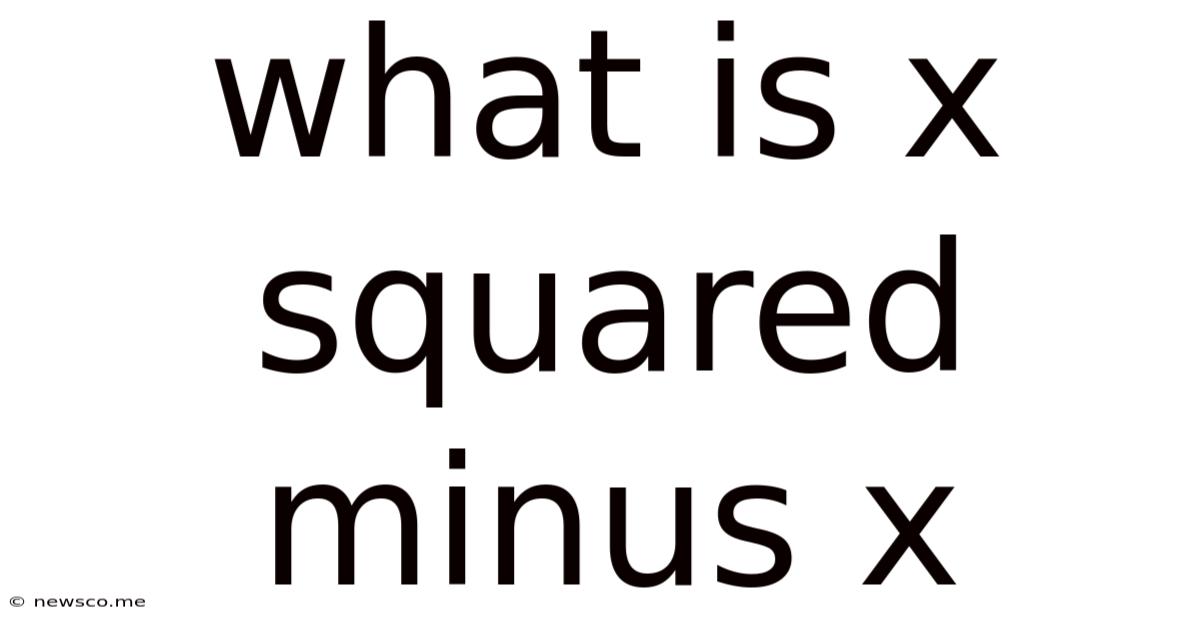
Table of Contents
What is x Squared Minus x? A Deep Dive into Quadratic Expressions
The seemingly simple expression "x squared minus x" opens a door to a vast world of mathematical concepts. While it might appear basic at first glance, understanding its properties, applications, and underlying principles is crucial for anyone pursuing mathematics, science, engineering, or even finance. This comprehensive guide will explore this quadratic expression, examining its graphical representation, factoring techniques, solving methods, and real-world applications.
Understanding the Expression: x² - x
The expression "x squared minus x," mathematically represented as x² - x, is a quadratic expression. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, 'x') is 2. It's a fundamental building block in algebra and forms the basis for understanding many more complex mathematical concepts. We can also express it as:
- x² - x = 0 (This represents the equation where the expression equals zero, leading to solving for the roots or zeros of the quadratic.)
- f(x) = x² - x (This represents the expression as a function, where 'f(x)' is the output for a given input 'x'.)
Let's break down the components:
- x²: This term represents 'x' multiplied by itself (x * x). It's a squared term, indicating a parabolic shape when graphed.
- -x: This term represents the negative of 'x' ( -1 * x). It is a linear term.
- The constant term: Notice that there is no constant term in this particular quadratic. A constant term is a number without a variable (e.g., in x² + 3x + 2, '2' is the constant term). The absence of a constant term has implications for its graph and roots.
Graphing x² - x
Visualizing the expression is crucial for grasping its behaviour. Plotting the function f(x) = x² - x on a Cartesian coordinate system reveals a parabola.
Key Features of the Graph:
- Parabola: The graph is a U-shaped curve, characteristic of quadratic functions. The parabola opens upwards because the coefficient of the x² term (which is 1) is positive. If the coefficient were negative, the parabola would open downwards.
- Vertex: The vertex is the lowest point on the parabola (the minimum value of the function). For the function f(x) = x² - x, the vertex can be found using the formula for the x-coordinate of the vertex of a parabola: x = -b / 2a, where a = 1 and b = -1 (coefficients of the x² and x terms, respectively). In this case, the x-coordinate of the vertex is x = 1/2. Substituting this back into the equation gives the y-coordinate: f(1/2) = (1/2)² - (1/2) = -1/4. Therefore, the vertex is at (1/2, -1/4).
- x-intercepts (Roots or Zeros): These are the points where the parabola intersects the x-axis (where y = 0 or f(x) = 0). To find the x-intercepts, we solve the equation x² - x = 0. Factoring the expression, we get x(x - 1) = 0. This gives us two solutions: x = 0 and x = 1. These are the x-intercepts, meaning the parabola crosses the x-axis at (0, 0) and (1, 0).
- y-intercept: This is the point where the parabola intersects the y-axis (where x = 0). Substituting x = 0 into the equation gives f(0) = 0² - 0 = 0. The y-intercept is at (0, 0). Notice that in this case, the x-intercept and y-intercept are the same point.
Factoring x² - x
Factoring a quadratic expression involves rewriting it as a product of simpler expressions. Factoring is crucial for solving quadratic equations and simplifying more complex algebraic expressions. The expression x² - x can be factored simply by taking out the common factor 'x':
x² - x = x(x - 1)
This factored form highlights that the expression is the product of 'x' and '(x - 1)'. This factorization directly leads to the solutions of the equation x² - x = 0, as explained in the previous section.
Solving Quadratic Equations: x² - x = 0
Solving a quadratic equation means finding the values of 'x' that make the equation true. The equation x² - x = 0 is a simple quadratic equation, and there are several methods to solve it:
1. Factoring:
As we have already seen, factoring the expression gives x(x - 1) = 0. For this equation to be true, either x = 0 or x - 1 = 0. Therefore, the solutions are x = 0 and x = 1.
2. Quadratic Formula:
The quadratic formula is a general method for solving any quadratic equation of the form ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
In our case, a = 1, b = -1, and c = 0. Substituting these values into the formula gives:
x = [1 ± √((-1)² - 4 * 1 * 0)] / (2 * 1) = [1 ± √1] / 2
This leads to the same solutions: x = 0 and x = 1.
3. Completing the Square:
Completing the square is another algebraic technique for solving quadratic equations. While it's a bit more involved than factoring or using the quadratic formula for this specific equation, it's a valuable technique for solving more complex quadratics.
Applications of x² - x
While seemingly simple, the expression x² - x and its related concepts find applications in various fields:
- Physics: Quadratic equations often model projectile motion. The height of a projectile over time might be described by a quadratic equation similar in form to x² - x, though with added constants that account for factors like gravity and initial velocity.
- Engineering: In structural engineering, quadratic equations can be used to calculate stresses and strains in beams and other structural components.
- Economics and Finance: Quadratic functions can be used to model economic phenomena such as profit maximization, cost minimization, and supply and demand curves.
- Computer Science: Quadratic equations are used in algorithms and optimization problems.
- Calculus: Understanding quadratic functions is fundamental for learning about derivatives and integrals, which are crucial tools in calculus.
- Geometry: Quadratic equations can be used to solve geometric problems related to areas and volumes of various shapes.
Extensions and Further Exploration
The exploration of x² - x can extend to more complex concepts:
- Complex Numbers: If we were to consider the equation x² - x = k (where k is a constant), and k were to have a certain value the solutions for 'x' could become complex numbers, involving the imaginary unit 'i'.
- Inequalities: Instead of solving the equation x² - x = 0, we could explore the inequality x² - x > 0 or x² - x < 0, which would involve considering intervals on the number line where the quadratic expression is positive or negative.
- Higher-Degree Polynomials: The principles of solving quadratic equations extend to solving higher-degree polynomials, though these often become more complicated.
Conclusion: Beyond the Basics
The expression x² - x, while appearing straightforward, serves as a gateway to understanding fundamental mathematical concepts. From its graphical representation as a parabola to its various methods of solution and broad applications, it demonstrates the power and versatility of quadratic expressions. A deep understanding of this simple expression builds a solid foundation for tackling more advanced mathematical challenges across numerous disciplines. Remember to practice solving various quadratic equations, graphing different quadratic functions, and exploring their applications in relevant fields to solidify your understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is X Squared Minus X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.