What Is X Squared Minus X Squared
News Co
Apr 21, 2025 · 5 min read
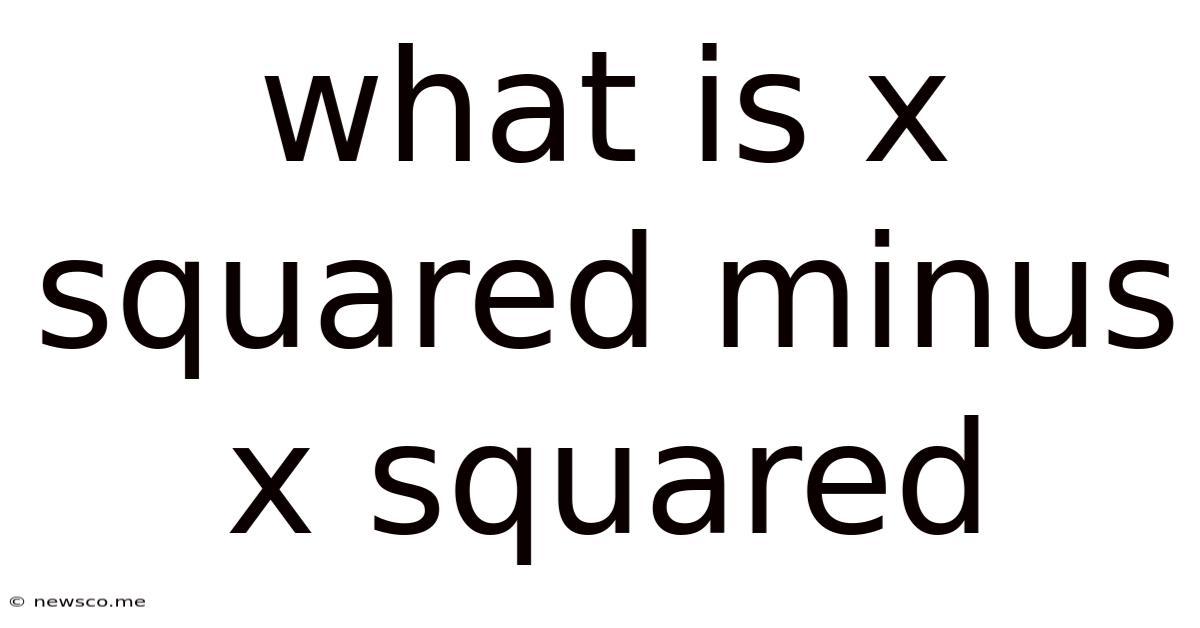
Table of Contents
What is x Squared Minus x Squared? A Deep Dive into Algebraic Simplification
The seemingly simple question, "What is x squared minus x squared?", opens a door to a fascinating exploration of fundamental algebraic concepts. While the immediate answer might seem obvious, delving deeper reveals crucial insights into mathematical principles and their practical applications. This article will unpack this seemingly straightforward problem, examining its solution, its implications, and its relevance in broader mathematical contexts.
Understanding the Basics: Variables and Exponents
Before tackling the core question, let's solidify our understanding of the foundational elements involved: variables and exponents.
Variables: Representing the Unknown
In algebra, variables are symbolic representations of unknown quantities. They are typically denoted by letters, most commonly x, y, and z. These variables can represent any number, allowing us to create general formulas and equations applicable to a wide range of situations. In our problem, "x" represents an unknown value.
Exponents: Indicating Repeated Multiplication
Exponents, also known as powers or indices, indicate repeated multiplication. For example, x² (x squared) means x multiplied by itself: x * x. Similarly, x³ (x cubed) would be x * x * x, and so on. The exponent indicates how many times the base (in this case, x) is multiplied by itself.
Solving x² - x²: A Step-by-Step Approach
Now, let's directly address the core question: What is x² - x²?
The expression x² - x² represents the subtraction of x² from x². This is a straightforward algebraic simplification problem. Since both terms are identical, subtracting one from the other results in zero.
Therefore, x² - x² = 0
This seemingly simple result has significant implications, demonstrating the fundamental principle of combining like terms in algebra.
Expanding the Concept: Like Terms and Algebraic Simplification
The solution to x² - x² highlights the importance of understanding like terms in algebra. Like terms are terms that have the same variables raised to the same powers. In our case, both x² terms are like terms. Algebraic simplification relies heavily on the ability to combine like terms through addition or subtraction.
Consider a slightly more complex example:
3x² + 5x² - 2x²
Here, all three terms are like terms (they all contain x²). We can simplify this expression by combining the coefficients (the numbers in front of the variables):
3 + 5 - 2 = 6
Therefore, 3x² + 5x² - 2x² = 6x²
This demonstrates how the principle of combining like terms extends beyond the simple case of x² - x² = 0.
Beyond the Basics: Applications in More Complex Equations
The fundamental principle illustrated by x² - x² = 0 is applicable in significantly more complex algebraic scenarios. Let's explore some examples:
Quadratic Equations
Quadratic equations are equations of the form ax² + bx + c = 0, where a, b, and c are constants. Solving quadratic equations often involves manipulating terms and simplifying expressions. Understanding how to combine like terms, as demonstrated by the x² - x² example, is crucial for successfully solving these equations. Techniques like completing the square or using the quadratic formula heavily rely on the ability to simplify expressions.
Polynomial Simplification
Polynomials are algebraic expressions consisting of multiple terms involving variables raised to non-negative integer powers. Simplifying polynomials involves combining like terms, a process directly related to our core example. Consider the following polynomial:
2x³ + 5x² - 3x² + 7x - 4x + 1
Here, we can combine the like terms involving x² and x:
5x² - 3x² = 2x²
7x - 4x = 3x
Thus, the simplified polynomial becomes:
2x³ + 2x² + 3x + 1
This example again underscores the pervasive nature of combining like terms in algebraic simplification, directly connected to the basic principle illustrated by x² - x² = 0.
Calculus and Derivatives
The principle of simplifying algebraic expressions, and the concept of like terms, extends even into the realm of calculus. When calculating derivatives, we often need to simplify complex expressions involving variables and exponents. The ability to quickly and accurately simplify such expressions is essential for efficient and correct calculation of derivatives. The foundational understanding gained from simplifying simple expressions like x² - x² directly contributes to this more advanced mathematical skill.
Practical Applications: Real-World Scenarios
The seemingly abstract concept of simplifying algebraic expressions, and the simple case of x² - x², finds applications in a variety of real-world scenarios. Here are a few examples:
- Physics: Many physics equations involve variables and exponents. Simplifying these equations is crucial for understanding and solving problems related to motion, forces, energy, and more.
- Engineering: Engineers use algebraic equations to model and solve problems in structural design, electrical circuits, fluid dynamics, and numerous other fields. The ability to simplify expressions efficiently is vital for accurate and efficient problem-solving.
- Finance: Financial modeling often involves using equations to calculate interest, investments, and other financial metrics. Simplifying complex expressions helps in making informed financial decisions.
- Computer Science: In computer programming and algorithms, manipulating and simplifying algebraic expressions is vital for writing efficient and correct code. The principles learned from elementary algebraic operations are fundamental to higher level programming concepts.
Conclusion: The Significance of Fundamentals
The answer to the seemingly simple question, "What is x squared minus x squared?", is 0. However, this seemingly trivial solution provides a crucial gateway to understanding fundamental concepts in algebra, such as like terms and algebraic simplification. This understanding extends far beyond basic algebra, forming the foundation for more advanced mathematical concepts used across various disciplines, including physics, engineering, finance, and computer science. Mastering these fundamental principles is essential for success in various fields and underscores the power of seemingly simple mathematical ideas. The ability to accurately and efficiently simplify algebraic expressions, rooted in the understanding that x² - x² = 0, is a skill of immense practical and theoretical value. It highlights the importance of building a solid foundation in mathematics, showing that even the simplest concepts can be crucial building blocks for complex and significant understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is X Squared Minus X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.