What Is X To The 1 2
News Co
Mar 23, 2025 · 6 min read
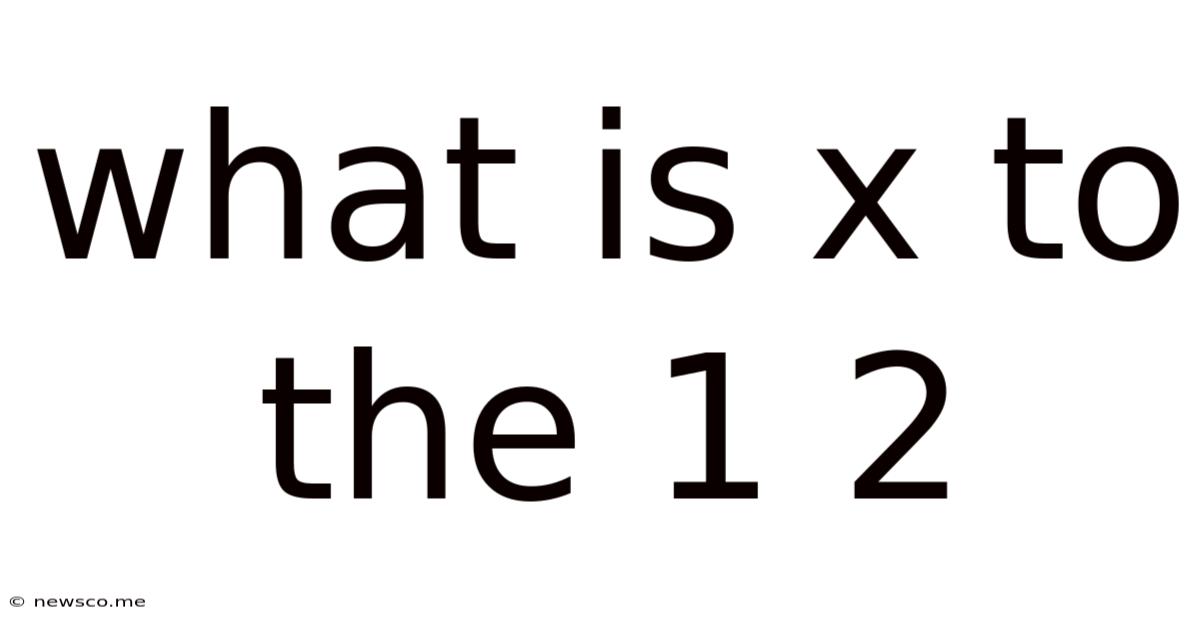
Table of Contents
What is x to the 1/2? Understanding Square Roots and Fractional Exponents
Understanding exponents is fundamental to mathematics and many scientific fields. While integer exponents (like x², x³, x⁴) are relatively straightforward, fractional exponents can seem more confusing at first glance. This article delves into the meaning of "x to the 1/2," explaining what it represents, how it relates to square roots, and its broader significance within the realm of mathematics. We'll explore its applications, provide examples, and clarify common misconceptions.
Decoding x<sup>1/2</sup>: The Square Root
The expression "x to the 1/2," often written as x<sup>1/2</sup>, is mathematically equivalent to the square root of x. In simpler terms, it's the number that, when multiplied by itself, equals x. The square root symbol (√) is another way to represent this operation. Therefore:
x<sup>1/2</sup> = √x
This means that finding the value of x<sup>1/2</sup> involves finding a number that, when squared (multiplied by itself), gives you x. For example:
- 4<sup>1/2</sup> = √4 = 2 (because 2 * 2 = 4)
- 9<sup>1/2</sup> = √9 = 3 (because 3 * 3 = 9)
- 16<sup>1/2</sup> = √16 = 4 (because 4 * 4 = 16)
The Significance of the 1/2 Exponent
The fractional exponent 1/2 elegantly connects the concept of exponents with the concept of roots. The numerator (1) indicates the power to which the base (x) is raised, while the denominator (2) indicates the root to be taken. This generalizes to other fractional exponents:
- x<sup>1/3</sup> = ∛x (the cube root of x)
- x<sup>1/4</sup> = ∜x (the fourth root of x)
- x<sup>1/n</sup> = <sup>n</sup>√x (the nth root of x)
This demonstrates a fundamental property of exponents and radicals, offering a unified way to express both operations.
Beyond the Basics: Expanding the Understanding
The simplicity of x<sup>1/2</sup> = √x belies its deeper mathematical implications. Let's explore these:
Properties of Exponents and Fractional Exponents
Fractional exponents obey the same rules as integer exponents. This means that we can apply familiar exponent rules such as:
-
x<sup>a</sup> * x<sup>b</sup> = x<sup>a+b</sup>: This holds true for fractional exponents as well. For instance: x<sup>1/2</sup> * x<sup>1/2</sup> = x<sup>1/2 + 1/2</sup> = x<sup>1</sup> = x. This confirms our understanding that x<sup>1/2</sup> multiplied by itself equals x.
-
(x<sup>a</sup>)<sup>b</sup> = x<sup>ab</sup>: Again, this applies to fractions. (x<sup>1/2</sup>)<sup>2</sup> = x<sup>(1/2)*2</sup> = x<sup>1</sup> = x. This further reinforces the connection between the square root and the 1/2 exponent.
-
x<sup>a</sup> / x<sup>b</sup> = x<sup>a-b</sup>: This rule also holds for fractional exponents.
Understanding these properties is crucial for manipulating and simplifying expressions involving fractional exponents.
Dealing with Negative Numbers
When dealing with square roots (and, by extension, x<sup>1/2</sup>), the issue of negative numbers arises. The principal square root of a positive number is always positive. For example, √9 = 3, not -3, even though (-3)² = 9. However, the equation x² = 9 has two solutions: x = 3 and x = -3.
In the realm of complex numbers, we can extend the concept of square roots to include negative numbers. The square root of a negative number involves the imaginary unit i, where i² = -1. For example:
√-9 = √(9 * -1) = 3i
Therefore, while the principal square root of a negative number isn't a real number, it can be expressed using complex numbers.
Applications of x<sup>1/2</sup>
The square root (and thus x<sup>1/2</sup>) has widespread applications across diverse fields:
-
Geometry: Calculating distances, areas, and volumes frequently involve square roots (e.g., the Pythagorean theorem).
-
Physics: Numerous physical laws and equations include square roots, such as equations related to velocity, acceleration, and energy.
-
Statistics: Standard deviation and other statistical measures often utilize square roots.
-
Computer Graphics: Transformations and calculations within computer graphics often use square roots.
-
Finance: Compound interest calculations sometimes use square roots.
These examples showcase how fundamental the concept of x<sup>1/2</sup> is in various quantitative disciplines.
Advanced Concepts and Extensions
Let's delve into some more advanced aspects of x<sup>1/2</sup>:
Fractional Exponents with Numerators Other Than 1
The concept extends beyond the 1/2 exponent. Consider x<sup>m/n</sup>. This can be interpreted as:
(x<sup>m</sup>)<sup>1/n</sup> = <sup>n</sup>√(x<sup>m</sup>)
Or equivalently:
(<sup>n</sup>√x)<sup>m</sup>
Both expressions are equivalent and offer different approaches to calculating the result.
Irrational Exponents
The exponent doesn't have to be rational (a fraction). It can be an irrational number such as π or √2. While calculating these might require numerical methods, the underlying principle remains the same.
Complex Numbers and Fractional Exponents
As mentioned, extending the concept to complex numbers allows us to deal with the square roots of negative numbers and opens up a whole new realm of mathematical possibilities.
Common Misconceptions and Pitfalls
Let's address some common misconceptions surrounding x<sup>1/2</sup>:
-
Confusing x<sup>1/2</sup> with x/2: These are fundamentally different. x<sup>1/2</sup> is the square root of x, while x/2 is half of x.
-
Ignoring Negative Solutions: When solving equations involving x<sup>1/2</sup>, remember there might be two solutions (positive and negative) if the context permits it.
-
Incorrect Application of Exponent Rules: Ensure you apply exponent rules correctly, especially when dealing with fractions and negative exponents.
Conclusion: Mastering the Square Root and Fractional Exponents
Understanding "x to the 1/2" as the square root of x is a key step in mastering fractional exponents. This concept is not merely an abstract mathematical idea; it's a cornerstone of countless applications across various fields. By grasping the fundamental principles outlined in this article, including the relationship between exponents and radicals, properties of exponents applied to fractions, and the handling of negative numbers, you can confidently approach and solve problems involving fractional exponents, laying a solid foundation for more advanced mathematical studies. Remember to practice, use the various methods of calculation, and always double-check your work to avoid common pitfalls. Through consistent practice and a deeper understanding of the underlying principles, you can confidently navigate the world of fractional exponents and their widespread applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is X To The 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.