What Number Is Next 2 7 8 3 12 9
News Co
Apr 16, 2025 · 5 min read
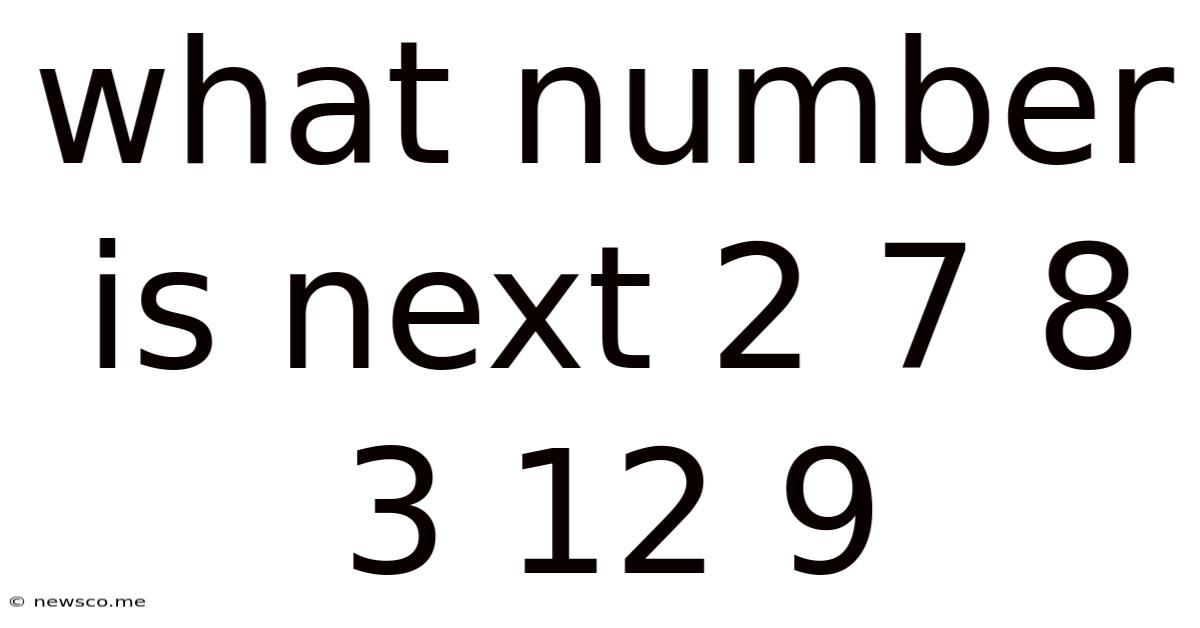
Table of Contents
What Number is Next? Unraveling the Sequence 2, 7, 8, 3, 12, 9
The seemingly simple question, "What number is next in the sequence 2, 7, 8, 3, 12, 9?", hides a fascinating challenge in logical reasoning and pattern recognition. There's no single definitive answer, as multiple patterns could potentially generate this sequence. This article will explore several possibilities, delve into the methodology of sequence analysis, and ultimately demonstrate how to approach such problems with a systematic and creative approach. Understanding these methods will equip you to tackle similar number sequences and strengthen your analytical skills.
The Allure of Number Sequences
Number sequences, like puzzles, captivate us with their inherent challenge. They demand careful observation, logical deduction, and a touch of creative thinking. The apparent randomness of a sequence often masks an underlying order, waiting to be uncovered. This process of discovery is intellectually stimulating, rewarding us with a sense of accomplishment and a deeper appreciation for mathematical patterns. The ability to identify patterns is also a valuable skill transferable to various fields, from data analysis and programming to finance and scientific research.
Analyzing the Sequence: 2, 7, 8, 3, 12, 9
Let's dissect the sequence 2, 7, 8, 3, 12, 9. Our goal is to identify a rule or pattern that consistently generates each number in the sequence. We'll explore several potential approaches:
Approach 1: Alternating Patterns
One common strategy is to examine the sequence in alternating terms. Let's look at the odd-numbered terms (2, 8, 12) and the even-numbered terms (7, 3, 9) separately.
-
Odd-numbered terms (2, 8, 12): Here, we notice a pattern of adding 6. 2 + 6 = 8; 8 + 4 = 12. The difference between consecutive terms is decreasing by 2 each time. Following this pattern, the next odd-numbered term would be 12 + 2 = 14.
-
Even-numbered terms (7, 3, 9): This pattern seems less obvious. The differences are -4 and +6. No immediately apparent consistent rule emerges. We could speculate that the pattern alternates between subtracting and adding, with increasing magnitudes. If so, the next difference might be +8, leading to 9 + 8 = 17.
This approach suggests a possible next number in the sequence, but it is not entirely consistent and requires further investigation.
Approach 2: Differences and Second Differences
Another powerful technique involves analyzing the differences between consecutive terms. This method often reveals hidden patterns, especially in sequences with polynomial relationships.
Let's calculate the first differences:
- 7 - 2 = 5
- 8 - 7 = 1
- 3 - 8 = -5
- 12 - 3 = 9
- 9 - 12 = -3
The first differences (5, 1, -5, 9, -3) don't immediately show a clear pattern. Let's calculate the second differences (differences between the first differences):
- 1 - 5 = -4
- -5 - 1 = -6
- 9 - (-5) = 14
- -3 - 9 = -12
Again, no obvious pattern emerges. This approach, while useful in many cases, doesn't yield a simple solution for this particular sequence.
Approach 3: Modular Arithmetic
Modular arithmetic examines remainders after division. Let's consider the remainders when each number is divided by a specific integer. For example, let's look at remainders when dividing by 5:
- 2 % 5 = 2
- 7 % 5 = 2
- 8 % 5 = 3
- 3 % 5 = 3
- 12 % 5 = 2
- 9 % 5 = 4
This doesn't immediately reveal a consistent pattern. However, experimenting with other moduli might yield a more revealing result. The absence of a clear pattern here doesn't rule out the possibility of modular arithmetic being relevant; further exploration with different moduli might uncover a pattern.
Approach 4: Combination of Operations
It's possible that the sequence involves a combination of arithmetic operations, potentially involving multiple steps or alternating operations. For example, one might speculate about adding and subtracting, or multiplying and dividing in a particular order. However, without a clear pattern in the differences or remainders, identifying such a combination becomes difficult and requires a more methodical approach with trial and error.
Approach 5: Hidden Functions or Relationships
Sometimes, a sequence might be generated by a more complex mathematical function or relationship that isn't immediately apparent. This could involve exponential functions, trigonometric functions, or even recursive relationships where a term depends on previous terms in a non-linear way.
The Importance of Context and Additional Information
The difficulty in finding a single solution highlights the importance of context when dealing with number sequences. If this sequence came from a specific problem or puzzle, additional information could significantly narrow down the possibilities. Knowing the source or the intended pattern could reveal clues that are otherwise hidden.
For example, if this sequence represents measurements in a physical system, the underlying principles governing that system might impose constraints on the possible patterns. Similarly, if the sequence represents coded information, deciphering the code requires additional knowledge of the encoding scheme.
Conclusion: Multiple Solutions and the Power of Exploration
The sequence 2, 7, 8, 3, 12, 9 does not have a single, universally accepted next number. We have explored several approaches, demonstrating that multiple patterns could plausibly generate the sequence. This ambiguity underscores the importance of systematic analysis, creativity, and the consideration of multiple perspectives when tackling such problems. The process of exploration, even when it doesn't lead to a definitive "correct" answer, sharpens our analytical skills and expands our understanding of mathematical patterns.
This exercise is a testament to the rich complexity hidden within seemingly simple number sequences. While we haven't found a definitive answer, the process of attempting to solve this problem has highlighted various analytical methods and the value of exploring different approaches when faced with a mathematical puzzle. The exploration itself is often as rewarding as finding a definitive solution. Remember, the journey of discovery is as crucial as the destination.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Number Is Next 2 7 8 3 12 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.