What Number Must You Add To Complete The Square
News Co
Apr 05, 2025 · 6 min read
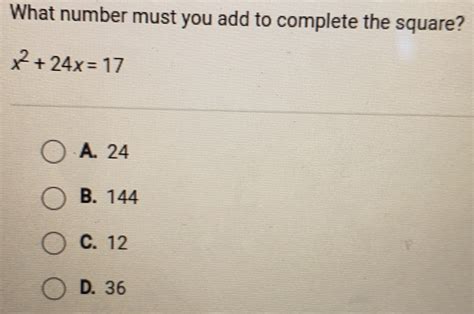
Table of Contents
Completing the Square: A Comprehensive Guide
Completing the square is a crucial algebraic technique used to solve quadratic equations, simplify expressions, and even graph parabolas. While the process might seem daunting at first, understanding the underlying principles makes it straightforward and applicable to a wide range of mathematical problems. This comprehensive guide will delve into the intricacies of completing the square, providing step-by-step instructions, examples, and explanations to solidify your understanding.
Understanding Quadratic Equations and Their Forms
Before diving into completing the square, let's revisit quadratic equations. A quadratic equation is an equation of the form:
ax² + bx + c = 0
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. This is the standard form. However, we can also represent quadratic equations in other forms, such as the vertex form, which is particularly useful for graphing:
a(x - h)² + k = 0
where (h, k) represents the vertex of the parabola. Completing the square is the bridge that connects the standard form to the vertex form.
The Mechanics of Completing the Square
The core idea behind completing the square is to manipulate a quadratic expression in standard form (ax² + bx + c) into a perfect square trinomial, which can be factored as (x + p)². A perfect square trinomial is a trinomial (a three-term expression) that can be factored into the square of a binomial. For example, x² + 6x + 9 is a perfect square trinomial because it factors to (x + 3)².
To achieve this, we focus on the first two terms of the quadratic expression (ax² + bx). The steps are as follows:
-
Ensure the coefficient of x² is 1: If the coefficient of x² (a) is not 1, factor it out from the first two terms.
-
Find half of the coefficient of x: Take half of the coefficient of x (b), which is b/2.
-
Square the result: Square the value obtained in step 2, which gives (b/2)².
-
Add and subtract the result: Add (b/2)² to the expression inside the parentheses (if you factored out a coefficient in step 1) and subtract it outside the parentheses to maintain the equality. This is the crucial step where we "complete the square."
-
Factor the perfect square trinomial: The first three terms within the parentheses will now form a perfect square trinomial that can be factored as (x + b/2)².
-
Simplify: Simplify the expression by combining constant terms outside the parentheses.
Step-by-Step Examples
Let's illustrate the process with several examples of varying complexity.
Example 1: Simple Case
Complete the square for x² + 6x + 2 = 0
-
The coefficient of x² is already 1.
-
Half of the coefficient of x (6) is 6/2 = 3.
-
Squaring the result gives 3² = 9.
-
Add and subtract 9: x² + 6x + 9 - 9 + 2 = 0
-
Factor the perfect square trinomial: (x + 3)² - 7 = 0
-
Simplified form: (x + 3)² = 7
Example 2: With a Leading Coefficient Other Than 1
Complete the square for 2x² + 8x - 10 = 0
-
Factor out the coefficient of x² (2) from the first two terms: 2(x² + 4x) - 10 = 0
-
Half of the coefficient of x (4) is 4/2 = 2.
-
Squaring the result gives 2² = 4.
-
Add and subtract 4 inside the parenthesis: 2(x² + 4x + 4 - 4) - 10 = 0
-
Distribute the 2 and factor the perfect square trinomial: 2(x + 2)² - 8 - 10 = 0
-
Simplify: 2(x + 2)² - 18 = 0 or 2(x + 2)² = 18
Example 3: Dealing with Fractions
Complete the square for x² + 5x + 1 = 0
-
Coefficient of x² is 1.
-
Half of the coefficient of x (5) is 5/2.
-
Squaring the result gives (5/2)² = 25/4.
-
Add and subtract 25/4: x² + 5x + 25/4 - 25/4 + 1 = 0
-
Factor the perfect square trinomial: (x + 5/2)² - 21/4 = 0
-
Simplified form: (x + 5/2)² = 21/4
Applications of Completing the Square
Completing the square isn't just a theoretical exercise; it has numerous practical applications in various areas of mathematics and beyond:
-
Solving Quadratic Equations: The most common use is solving quadratic equations that cannot be easily factored. By completing the square, you can rewrite the equation in a form that allows you to solve for x directly.
-
Finding the Vertex of a Parabola: The vertex form of a quadratic equation, obtained through completing the square, directly reveals the coordinates of the parabola's vertex (h, k). This is invaluable in graphing and analyzing quadratic functions.
-
Deriving the Quadratic Formula: The widely used quadratic formula is actually derived through the process of completing the square on the general quadratic equation ax² + bx + c = 0.
-
Calculus: Completing the square is frequently used in calculus for integrating certain functions and simplifying expressions involving quadratic terms.
-
Statistics: Completing the square plays a role in some statistical calculations, particularly those involving normal distributions.
Common Mistakes to Avoid
While completing the square is a powerful technique, some common mistakes can lead to incorrect results. Here are a few points to watch out for:
-
Incorrectly handling the leading coefficient: Failure to properly factor out the leading coefficient (a) before completing the square can lead to significant errors.
-
Forgetting to add and subtract the same value: Adding (b/2)² to one side of the equation without subtracting it from the other side will disrupt the equality and yield an incorrect result.
-
Errors in factoring the perfect square trinomial: Care must be taken to ensure the perfect square trinomial is factored correctly.
-
Arithmetic mistakes: Simple arithmetic errors can easily creep in, especially when dealing with fractions or larger numbers. Always double-check your calculations.
Advanced Applications and Extensions
The principles of completing the square can be extended to solve more complex problems. For instance:
-
Completing the square with complex numbers: The technique can be adapted to work with quadratic equations involving complex numbers.
-
Solving quadratic equations in more than one variable: Completing the square can be used to solve certain types of quadratic equations with more than one variable.
Conclusion
Completing the square, although initially seeming complex, is a fundamental algebraic technique with wide-ranging applications. Mastering this skill is essential for understanding quadratic equations and related concepts in algebra, calculus, and other areas of mathematics. By following the step-by-step procedure and carefully avoiding common mistakes, you can confidently apply completing the square to solve a variety of problems and unlock a deeper understanding of quadratic functions. Consistent practice and careful attention to detail are key to mastering this valuable algebraic tool. Remember to always double-check your work and make use of the examples provided to reinforce your understanding. With perseverance, completing the square will become second nature, empowering you to tackle more challenging mathematical problems with confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Number Must You Add To Complete The Square . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.