What Percent Is 20 Of 30
News Co
Mar 24, 2025 · 5 min read
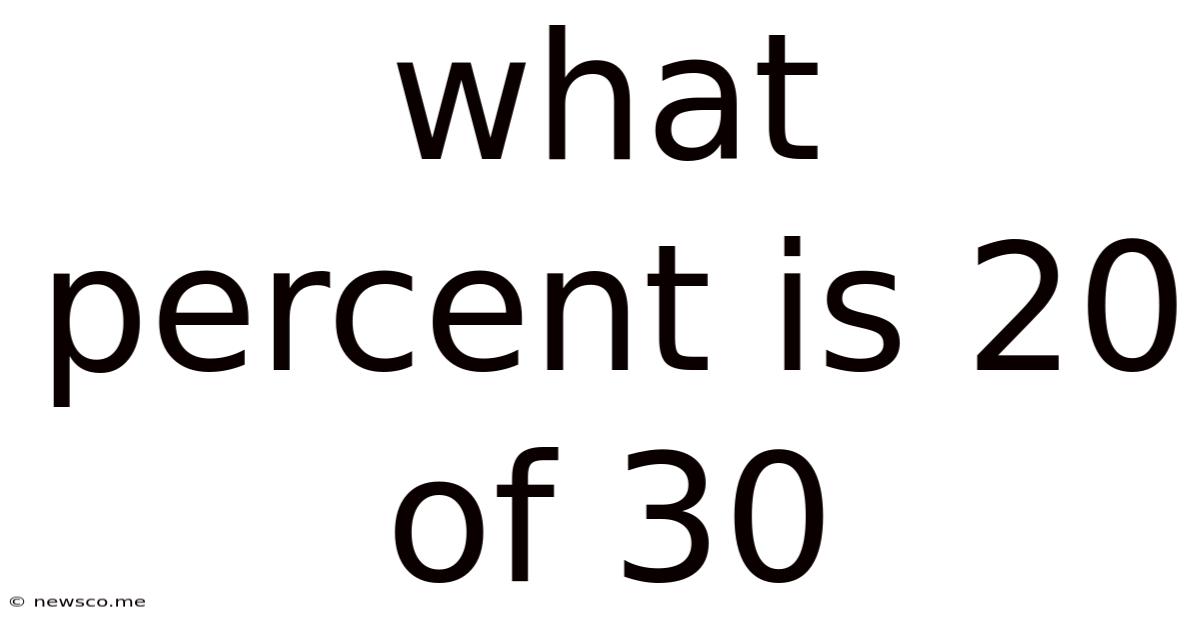
Table of Contents
What Percent is 20 of 30? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and sales tax to comprehending statistical data and financial reports. This comprehensive guide delves into the question, "What percent is 20 of 30?", providing a step-by-step explanation, exploring different calculation methods, and offering practical applications to solidify your understanding.
Understanding Percentages: The Basics
Before diving into the specific calculation, let's establish a solid foundation in percentage concepts. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100". For instance, 50% means 50 out of 100, or ½.
Key Terms:
- Percentage: The portion of a whole expressed as a number out of 100.
- Whole (or Base): The total amount or quantity you're considering.
- Part: The portion of the whole you're interested in expressing as a percentage.
Calculating "What Percent is 20 of 30?"
The question, "What percent is 20 of 30?" asks us to find what percentage 20 represents when compared to the whole, which is 30. We can solve this using several methods:
Method 1: Using the Formula
The most straightforward method employs the fundamental percentage formula:
(Part / Whole) x 100 = Percentage
In our case:
- Part = 20
- Whole = 30
Substituting these values into the formula:
(20 / 30) x 100 = 66.67%
Therefore, 20 is 66.67% of 30.
Method 2: Decimal Conversion
This method involves first converting the fraction (Part/Whole) into a decimal and then multiplying by 100 to express it as a percentage.
- Convert the fraction to a decimal: 20/30 = 0.6667 (approximately)
- Multiply by 100: 0.6667 x 100 = 66.67%
This method yields the same result: 20 is approximately 66.67% of 30.
Method 3: Proportion Method
This method uses proportions to solve the problem. We set up a proportion where x represents the unknown percentage:
x/100 = 20/30
To solve for x, we cross-multiply:
30x = 2000
x = 2000/30
x = 66.67%
Again, we arrive at the same answer: 20 is approximately 66.67% of 30.
Practical Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios. Here are a few examples:
1. Sales and Discounts:
Imagine a store offering a 20% discount on an item originally priced at $30. Using the knowledge gained above, you can easily calculate the discount amount and the final price.
- Discount amount: (20/100) x $30 = $6
- Final price: $30 - $6 = $24
2. Financial Calculations:
Percentages are crucial in finance. For instance, calculating interest rates, profit margins, and investment returns all rely on percentage calculations.
- Interest Calculation: If you invest $1000 at an annual interest rate of 5%, you can calculate the yearly interest earned as follows: (5/100) x $1000 = $50.
3. Data Analysis and Statistics:
Percentages are frequently used to represent data in a clear and concise manner. For instance, analyzing survey results, market share, or population demographics often involves expressing data as percentages. Consider a survey where 20 out of 30 respondents preferred a particular product. This translates to a 66.67% preference rate for that product.
4. Grading Systems:
Many academic institutions use a percentage-based grading system. For example, if you scored 20 out of 30 on a test, your score would be 66.67%.
5. Tax Calculations:
Sales tax is usually expressed as a percentage of the purchase price. Understanding percentages helps you determine the total cost, including tax.
Beyond the Basics: Handling More Complex Scenarios
While the example of "What percent is 20 of 30?" is relatively straightforward, percentage calculations can become more complex. Here are some variations and considerations:
1. Calculating the Whole (or Base):
Sometimes, you know the percentage and the part, and you need to find the whole. For instance, if you know that 20 represents 66.67% of a certain number, you can use the formula:
Whole = (Part / Percentage) x 100
In this case:
Whole = (20 / 66.67) x 100 ≈ 30
2. Calculating the Part:
Conversely, if you know the percentage and the whole, you can calculate the part. For example, if 20% of a number is 6, you can determine the number as follows:
Part = (Percentage / 100) x Whole
In this case:
Part = (20/100) x Whole = 6
Whole = 6 / (20/100) = 30
3. Percentage Increase and Decrease:
Calculating percentage increases and decreases is crucial in various financial and statistical contexts. For example, determining the percentage increase in sales from one year to the next or the percentage decrease in unemployment rates.
4. Compounding Percentages:
In situations involving multiple percentages, such as calculating compound interest or applying multiple discounts, it's important to understand how these percentages interact. Simply adding percentages together may not yield the correct result.
Mastering Percentage Calculations: Tips and Resources
Mastering percentage calculations takes practice and understanding. Here are some tips for improvement:
-
Practice regularly: The more you practice, the more confident and proficient you'll become. Solve various problems, starting with simple ones and gradually progressing to more complex scenarios.
-
Use online calculators and tools: Several online resources provide percentage calculators and tutorials that can assist you in learning and verifying your calculations.
-
Understand the underlying concepts: Focus on comprehending the principles of percentages, fractions, and decimals, which will significantly improve your problem-solving abilities.
-
Break down complex problems: If faced with a challenging problem, break it down into smaller, more manageable parts. This approach will make the calculation process more straightforward.
-
Check your work: Always review your calculations to ensure accuracy.
By consistently applying these tips and utilizing available resources, you can confidently handle percentage calculations in any situation. Remember, the key to mastering percentages lies in understanding the fundamental principles and practicing regularly. With time and dedication, you'll be able to tackle even the most complex percentage problems with ease.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Is 20 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.