What Percent Is 3 Of 5
News Co
Mar 28, 2025 · 4 min read
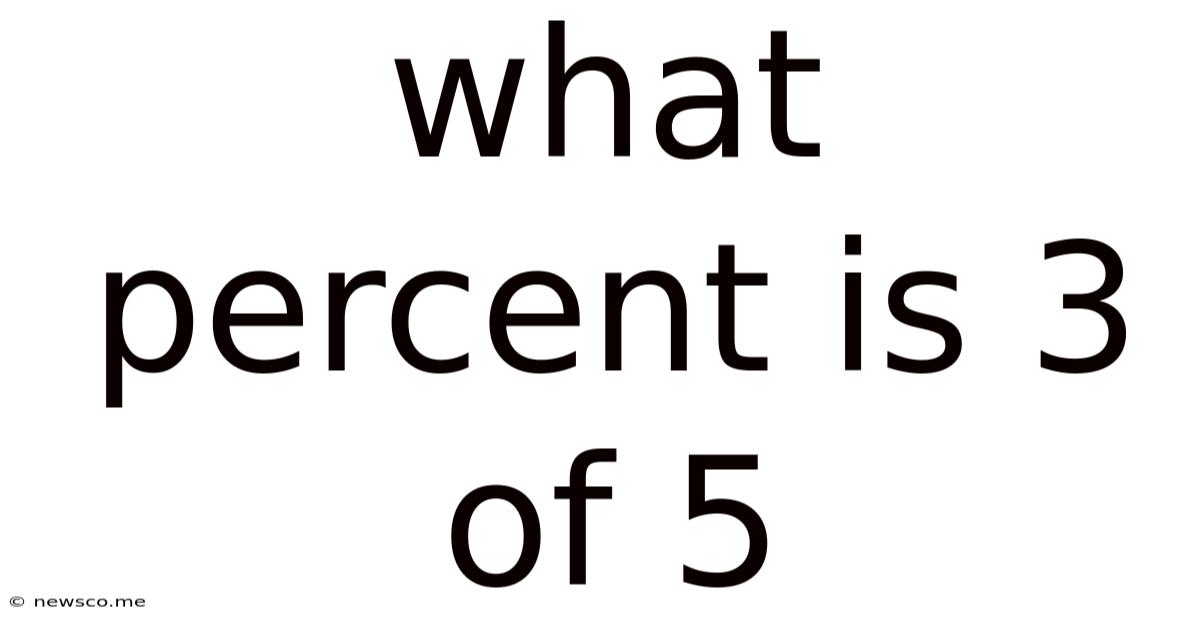
Table of Contents
What Percent is 3 of 5? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to interpreting statistics and analyzing financial data. This article delves deep into the question, "What percent is 3 of 5?", providing not only the answer but a comprehensive exploration of the underlying concepts, practical applications, and related calculations. We'll also look at different ways to solve this type of problem and explore the broader context of percentages within mathematics and real-world scenarios.
Calculating the Percentage: The Simple Method
The core question, "What percent is 3 of 5?", is essentially asking us to express the fraction 3/5 as a percentage. The formula for converting a fraction to a percentage is straightforward:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 3 (the number we're considering as a portion of the whole)
- Whole: 5 (the total number)
Substituting these values into the formula:
(3 / 5) * 100% = 60%
Therefore, 3 is 60% of 5.
Understanding the Concept of Percentage
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" ( per cent ). Percentages provide a standardized method for comparing proportions and making comparisons easier to understand. Instead of saying "3 out of 5," which might not be immediately intuitive in all contexts, stating "60%" provides a clear and concise representation.
Alternative Methods for Calculation
While the direct formula is the simplest, there are alternative approaches to solving this type of problem. These alternative methods can be helpful in building a deeper understanding and can be particularly useful when dealing with more complex percentage problems.
Method 2: Decimal Conversion
First, convert the fraction 3/5 into a decimal:
3 / 5 = 0.6
Then, multiply the decimal by 100% to express it as a percentage:
0.6 * 100% = 60%
Method 3: Proportion Method
This method uses proportions to find the unknown percentage. We set up a proportion:
3/5 = x/100
where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
5x = 300
x = 300 / 5
x = 60
Therefore, x = 60%, confirming our earlier result.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in many everyday situations. Here are some examples:
1. Discounts and Sales
Retail stores frequently advertise discounts as percentages. If a store offers a 20% discount on an item priced at $50, you can easily calculate the discount amount and the final price using percentage calculations. Understanding percentages helps you make informed purchasing decisions.
2. Taxes and Interest Rates
Governments impose various taxes, such as sales tax or income tax, often expressed as percentages. Similarly, interest rates on loans and savings accounts are also presented as percentages. Understanding these percentages is vital for managing personal finances effectively.
3. Statistics and Data Analysis
Percentages are frequently used to represent data in reports, charts, and graphs. For instance, understanding the percentage of people who prefer a certain product or the percentage change in a company's profits over time requires a solid grasp of percentage calculations. This is vital for interpreting data and making data-driven decisions.
4. Financial Investments
Understanding percentages is key to making informed decisions about investments. Calculating return on investment (ROI), analyzing stock market performance, and assessing the risks and rewards of different investment options all rely heavily on percentage calculations.
5. Grading Systems
Many educational institutions use percentages to represent student grades. Understanding the percentage score obtained on a test or assignment helps students assess their performance and identify areas for improvement. Teachers also use percentages to calculate final grades.
Advanced Percentage Problems and Concepts
While the "What percent is 3 of 5?" problem is relatively straightforward, percentage calculations can become more complex. Here are some advanced concepts:
1. Percentage Increase and Decrease
Calculating percentage increase or decrease involves finding the difference between two values and expressing it as a percentage of the original value. For example, if a stock price increases from $10 to $12, the percentage increase is calculated as:
((12 - 10) / 10) * 100% = 20%
2. Compound Interest
Compound interest involves calculating interest not only on the principal amount but also on the accumulated interest from previous periods. This concept is critical in understanding long-term investments and loan repayments.
3. Percentage Points vs. Percentages
It's crucial to distinguish between percentage points and percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase in the percentage itself. This distinction is crucial for accurate interpretation of data.
Conclusion: Mastering the Power of Percentages
The ability to calculate and understand percentages is an essential skill applicable across numerous disciplines and everyday situations. This article has provided a thorough examination of the question "What percent is 3 of 5?", demonstrating various calculation methods and exploring real-world applications. By mastering these concepts, you'll be better equipped to handle various quantitative challenges and make informed decisions in diverse areas of life, from personal finance to professional endeavors. Remember, understanding the core concepts and practicing regularly is key to becoming proficient in percentage calculations. Continue exploring further percentage-related problems and concepts to expand your understanding and confidently apply this valuable skill in your personal and professional life.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 3 Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.