What Percent Is 30 Of 40
News Co
Mar 19, 2025 · 5 min read
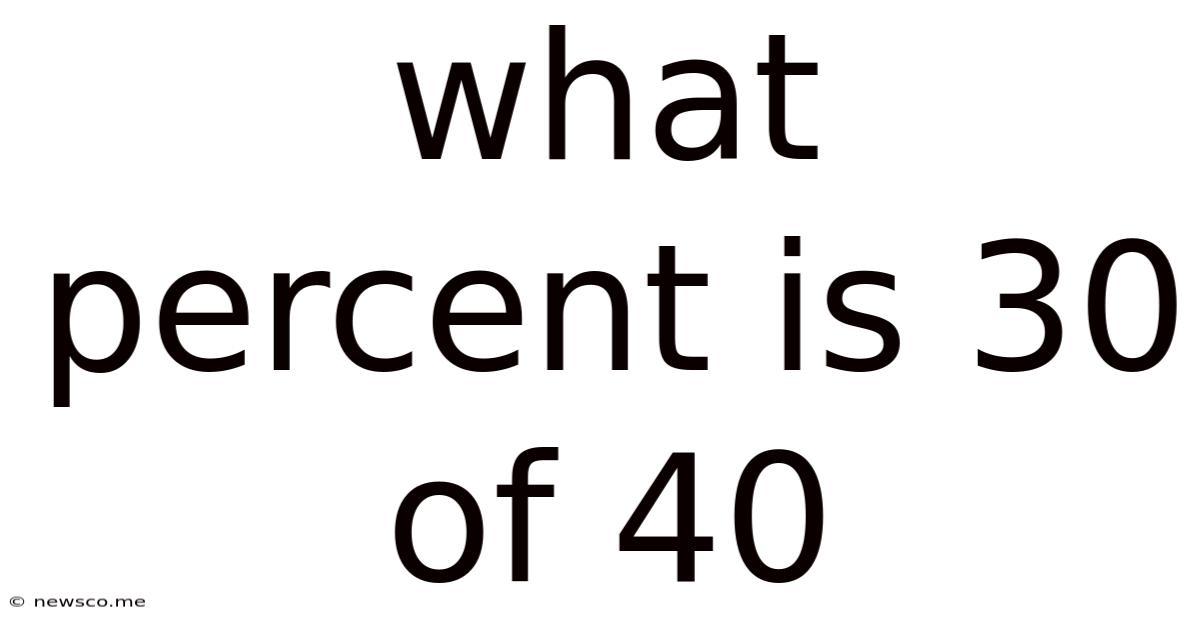
Table of Contents
What Percent is 30 of 40? A Deep Dive into Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications, from everyday budgeting and shopping to complex financial analyses and scientific research. Understanding how to determine what percent one number represents of another is crucial for navigating the numerical world. This comprehensive guide will explore how to calculate what percent 30 is of 40, providing various methods and demonstrating their practical applications. We'll go beyond the simple answer and delve into the underlying principles, offering examples and addressing potential misunderstandings along the way.
Understanding Percentages: The Foundation
Before we dive into the specific calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per hundred." For instance, 50% means 50 out of 100, which can also be written as 50/100 or 1/2 (one-half).
Method 1: The Fraction Method
The most straightforward way to determine what percent 30 is of 40 is to express the relationship as a fraction and then convert that fraction to a percentage.
-
Form the Fraction: The problem can be represented as the fraction 30/40. This fraction indicates that 30 is a part of the whole, which is 40.
-
Simplify the Fraction: To make the conversion easier, we simplify the fraction by finding the greatest common divisor (GCD) of 30 and 40, which is 10. Dividing both the numerator and the denominator by 10, we get 3/4.
-
Convert to Decimal: Now, we convert the simplified fraction 3/4 into a decimal by dividing the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
Convert to Percentage: To express the decimal as a percentage, we multiply it by 100: 0.75 x 100 = 75%.
Therefore, 30 is 75% of 40.
Method 2: The Proportion Method
This method utilizes the concept of proportions, setting up an equation to solve for the unknown percentage.
-
Set up the Proportion: We can represent the problem as a proportion:
x/100 = 30/40Here, 'x' represents the percentage we're trying to find. The proportion expresses the equivalence between the ratio of 30 to 40 and the ratio of x to 100 (since percentages are out of 100).
-
Cross-Multiply: Cross-multiply the terms to solve for x:
40x = 3000 -
Solve for x: Divide both sides of the equation by 40:
x = 3000/40 = 75
Therefore, x = 75%, confirming that 30 is 75% of 40.
Method 3: Using the Percentage Formula
The standard percentage formula can be applied directly:
Percentage = (Part/Whole) x 100
In our case:
Percentage = (30/40) x 100
Percentage = 0.75 x 100
Percentage = 75%
This method provides a concise and direct approach to calculating the percentage.
Real-World Applications: Illustrative Examples
Understanding percentage calculations extends beyond simple mathematical exercises. Let's look at practical scenarios where this skill is vital:
-
Sales and Discounts: A store offers a 25% discount on an item originally priced at $40. To find the discount amount, we calculate 25% of $40: (25/100) x $40 = $10. The discounted price would be $40 - $10 = $30. This calculation directly relates to the principle we've explored; it shows that $30 represents 75% of the original price.
-
Grade Calculations: A student scores 30 out of 40 points on a test. Using the methods described above, we can determine that the student's score is 75%. This allows for a clear understanding of their performance relative to the maximum possible score.
-
Financial Analysis: In investments, understanding percentage changes is critical. If an investment initially valued at $40 increases to $70, the percentage increase is calculated as follows: (($70-$40)/$40) x 100 = 75%. This signifies a 75% growth in the investment value.
-
Survey Results: Imagine a survey where 30 out of 40 respondents answered "yes" to a particular question. The percentage of "yes" responses is 75%, providing a concise representation of the survey results.
Addressing Common Misconceptions
While percentage calculations are relatively straightforward, some common misunderstandings can arise:
-
Confusing Part and Whole: It's crucial to identify the "part" and the "whole" correctly. In our example, 30 is the part, and 40 is the whole. Reversing these values will lead to an incorrect result.
-
Incorrect Decimal to Percentage Conversion: Remember to multiply the decimal by 100 to convert it into a percentage. Simply stating the decimal value as the percentage is a common mistake.
-
Overcomplicating the Calculation: While various methods exist, selecting the most efficient and easily understandable approach is crucial. For simple percentage calculations, the direct application of the formula often proves to be the most efficient.
Beyond the Basics: Advanced Percentage Applications
The fundamental principles discussed here form the basis for more complex percentage calculations:
-
Percentage Increase and Decrease: Calculating percentage changes, whether an increase or a decrease, involves similar principles. These are commonly used in financial analysis, statistics, and many other fields.
-
Compound Interest: Understanding compound interest relies heavily on percentage calculations, as interest accrues not only on the principal but also on accumulated interest.
-
Statistical Analysis: Percentages are frequently used in statistical data analysis to represent proportions, probabilities, and various other metrics.
-
Data Visualization: Percentages are often used to present data visually in charts and graphs, providing a clear and concise way to convey information.
Conclusion: Mastering Percentage Calculations
Understanding how to determine what percent 30 is of 40, and more generally, how to perform percentage calculations is an essential skill in various contexts. By mastering the methods outlined in this guide and understanding the underlying principles, you'll enhance your numerical literacy and confidently tackle percentage-related problems in your daily life and professional endeavors. The ability to accurately and efficiently calculate percentages is a valuable tool for making informed decisions and interpreting quantitative data effectively. Remember to carefully identify the part and the whole, apply the appropriate method, and always double-check your calculations to ensure accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Is 30 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.