What Percent Is 6 Of 8
News Co
Mar 17, 2025 · 5 min read
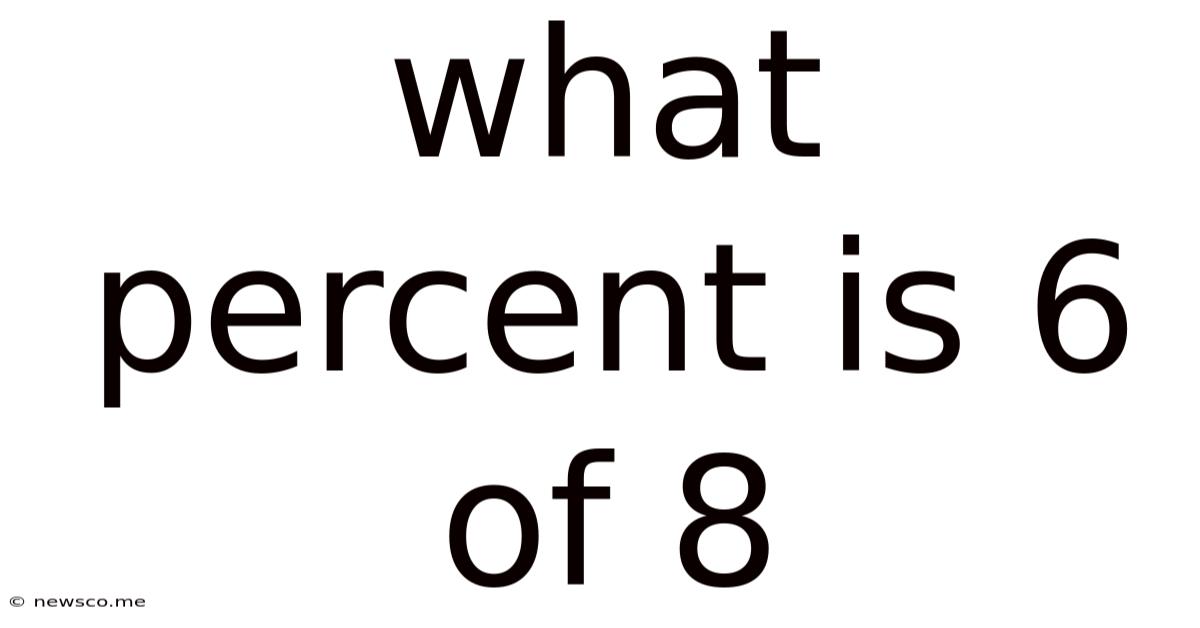
Table of Contents
What Percent is 6 of 8? A Deep Dive into Percentage Calculations
The seemingly simple question, "What percent is 6 of 8?" unlocks a world of practical applications in everyday life, from calculating discounts and tax rates to understanding statistics and analyzing data. This article will not only answer the question directly but also delve into the underlying concepts, providing a comprehensive guide to percentage calculations and their diverse uses.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5. Understanding this fundamental concept is crucial for grasping percentage calculations.
Key Terms:
- Percent (%): A symbol indicating a fraction of 100.
- Base: The total amount or whole quantity. In our example, the base is 8.
- Part: The portion of the base that is being expressed as a percentage. In our example, the part is 6.
- Percentage: The numerical value expressing the part as a fraction of the base (represented by the percentage symbol).
Calculating "What Percent is 6 of 8?"
The most straightforward way to calculate what percent 6 is of 8 is to use the following formula:
(Part / Base) x 100% = Percentage
Let's apply this to our question:
(6 / 8) x 100% = 75%
Therefore, 6 is 75% of 8.
Alternative Methods for Percentage Calculation
While the above formula is the most direct approach, there are other methods that can be equally effective, particularly when dealing with more complex scenarios or when mental calculations are preferred.
Method 2: Using Decimal Equivalents
This method involves converting the fraction into a decimal and then multiplying by 100.
- Convert the fraction: 6/8 simplifies to ¾.
- Convert to decimal: ¾ = 0.75
- Multiply by 100: 0.75 x 100% = 75%
Method 3: Proportions
Setting up a proportion can also help solve this type of problem:
- Let x represent the percentage: x/100 = 6/8
- Cross-multiply: 8x = 600
- Solve for x: x = 600/8 = 75
Therefore, x = 75%, confirming our previous result.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is indispensable in numerous real-world situations. Let's explore some key examples:
1. Retail and Sales:
- Discounts: A store offers a 25% discount on an item originally priced at $80. Calculating the discount amount involves finding 25% of $80, which is (25/100) x $80 = $20. The final price would be $80 - $20 = $60.
- Sales Tax: If the sales tax in a region is 6%, and you buy an item for $50, you calculate the tax as (6/100) x $50 = $3. The total cost including tax would be $50 + $3 = $53.
- Profit Margins: Businesses track their profit margins, expressing profit as a percentage of the cost of goods sold. For example, a profit margin of 20% means that for every $100 worth of goods sold, $20 is profit.
2. Finance and Investments:
- Interest Rates: Interest rates on loans and savings accounts are expressed as percentages. Understanding interest calculations is crucial for managing finances effectively.
- Investment Returns: The return on investments is often expressed as a percentage of the initial investment. For instance, a 10% return on a $1000 investment would be a profit of $100.
- Inflation: Inflation, the rate at which prices increase over time, is also expressed as a percentage.
3. Statistics and Data Analysis:
- Surveys and Polls: Data from surveys and polls are frequently represented using percentages to show the proportion of respondents who chose a particular option.
- Data Representation: Percentages are widely used in charts and graphs to visualize data effectively.
- Probability: Probabilities are often expressed as percentages, indicating the likelihood of an event occurring.
4. Everyday Life:
- Tip Calculation: When dining out, people often calculate a tip as a percentage of the total bill. A 15% tip on a $75 bill would be (15/100) x $75 = $11.25.
- Recipe Scaling: Adjusting recipes based on the number of servings requires calculating percentages to maintain the correct proportions of ingredients.
Beyond the Basics: More Complex Percentage Problems
While "What percent is 6 of 8?" is a straightforward example, the principles extend to more complex scenarios:
1. Finding the Base:
Sometimes, you know the percentage and the part, but need to find the base. For example, if 20% of a number is 10, what is the number? This can be solved using the formula:
- Base = (Part / Percentage) x 100
- Base = (10 / 20) x 100 = 50
2. Finding the Part:
If you know the percentage and the base, you can find the part. For example, what is 30% of 200? This is a simple multiplication:
- Part = (Percentage / 100) x Base
- Part = (30 / 100) x 200 = 60
3. Percentage Increase and Decrease:
Calculating percentage increases or decreases is frequently used in various contexts:
- Percentage Increase: [(New Value - Old Value) / Old Value] x 100%
- Percentage Decrease: [(Old Value - New Value) / Old Value] x 100%
Mastering Percentages: Tips and Practice
Becoming proficient in percentage calculations requires understanding the underlying principles and consistent practice. Here are some tips:
- Practice Regularly: Solve a variety of percentage problems to reinforce your understanding.
- Utilize Different Methods: Try different methods to approach the same problem to enhance your problem-solving skills.
- Use Online Resources: Several websites and apps offer interactive exercises and tutorials on percentage calculations.
- Real-World Application: Apply percentage calculations to real-life situations to make learning more engaging and relevant.
Conclusion
The seemingly simple question, "What percent is 6 of 8?", opens doors to a broader understanding of percentages and their widespread applications. By mastering percentage calculations, you equip yourself with a valuable skillset relevant across numerous fields, from personal finance to data analysis. This comprehensive guide has provided the tools and understanding to tackle a variety of percentage problems, empowering you to confidently navigate the world of numbers and percentages. Remember consistent practice is key to solidifying your skills and making percentage calculations second nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Is 6 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.