What Percent Is 9 Out Of 10
News Co
Apr 05, 2025 · 5 min read
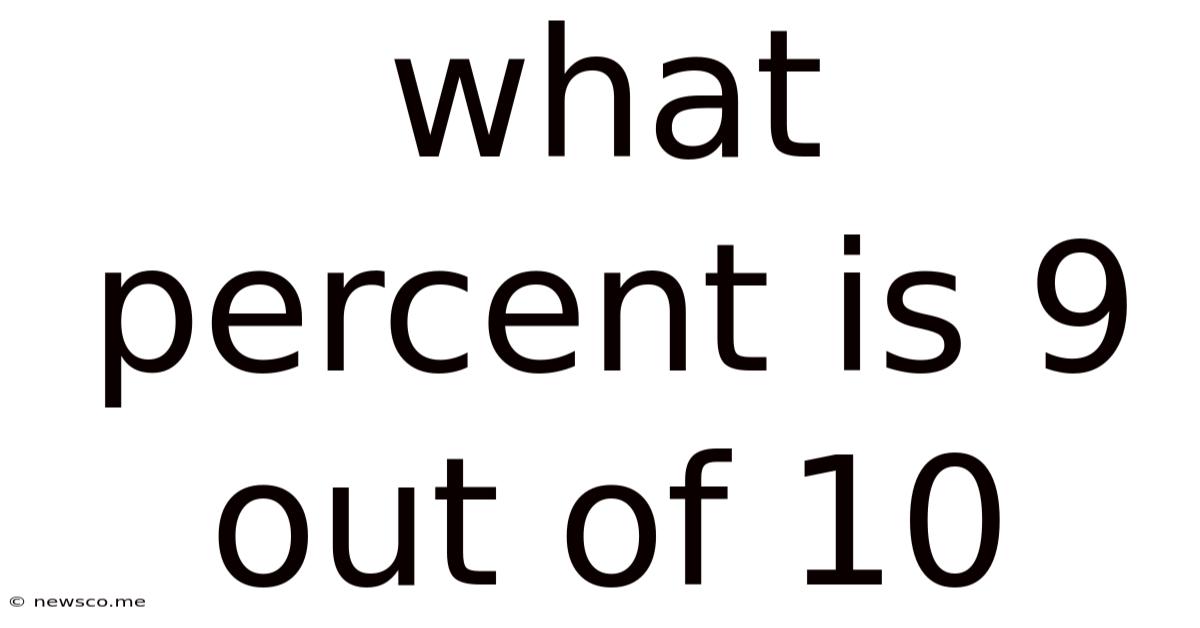
Table of Contents
What Percent is 9 out of 10? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts and taxes to comprehending statistical data and analyzing financial reports. This comprehensive guide will not only answer the question, "What percent is 9 out of 10?", but will also delve into the broader concept of percentages, exploring different methods of calculation and highlighting real-world applications.
Calculating the Percentage: 9 out of 10
The question, "What percent is 9 out of 10?" is essentially asking us to convert a fraction (9/10) into a percentage. There are several ways to approach this:
Method 1: Using the Fraction-to-Percentage Conversion Formula
The most straightforward method involves using the basic formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 9
- Whole: 10
Therefore, the calculation is:
(9 / 10) x 100% = 90%
Therefore, 9 out of 10 is 90%.
Method 2: Converting the Fraction to a Decimal
Another approach involves first converting the fraction 9/10 into a decimal. This is easily done by performing the division:
9 ÷ 10 = 0.9
Then, multiply the decimal by 100% to obtain the percentage:
0.9 x 100% = 90%
This method reinforces the understanding that percentages are essentially fractions expressed as parts per hundred.
Method 3: Understanding the Relationship Between Fractions, Decimals, and Percentages
This method emphasizes the interconnectedness between these three representations of a quantity. 9/10 represents nine-tenths of a whole. This translates to 0.9 as a decimal, signifying nine-tenths of one. Finally, multiplying by 100% transforms it into 90%, representing ninety parts per hundred. Understanding this relationship is crucial for efficient mathematical operations.
Beyond the Basics: Exploring Percentage Applications
While calculating 9 out of 10 as 90% is relatively simple, the concept of percentages extends far beyond basic arithmetic. Let's explore some real-world applications where understanding percentages becomes invaluable:
1. Financial Calculations: Interest Rates, Discounts, and Taxes
-
Interest Rates: Banks and financial institutions use percentages to express interest rates on loans, savings accounts, and investments. Understanding these percentages is crucial for making informed financial decisions. For instance, a 5% interest rate on a loan means you'll pay 5% of the principal amount as interest annually.
-
Discounts: Retail stores frequently offer discounts expressed as percentages. A 20% discount on a $100 item means you'll save $20 (20% of $100).
-
Taxes: Sales taxes and income taxes are levied as percentages of the purchase price or income. A 7% sales tax on a $50 purchase translates to an additional $3.50 in tax.
2. Data Analysis and Statistics: Representing Proportions and Trends
Percentages are essential in representing proportions and trends in data analysis and statistics. Consider the following scenarios:
-
Surveys and Polls: Survey results are often expressed as percentages to show the proportion of respondents who hold a particular opinion or preference. For example, a survey might reveal that 75% of respondents favor a particular policy.
-
Market Research: Market research studies frequently use percentages to analyze market share, customer demographics, and consumer preferences. Understanding these percentages helps companies make data-driven business decisions.
-
Scientific Studies: Percentages are frequently used in scientific studies to represent experimental results, statistical significance, and error margins. This allows researchers to communicate their findings in a clear and concise manner.
3. Everyday Life: Cooking, Measurement, and more
Percentages are not confined to complex mathematical or financial calculations. They appear frequently in everyday scenarios:
-
Cooking: Many recipes use percentages to describe the proportions of ingredients. For instance, a recipe might call for 60% flour and 40% water.
-
Measurement: Percentages can be used to express portions of a whole unit. For example, a partially filled container might contain 70% of its total capacity.
-
Grading Systems: Educational institutions often use percentages to represent student grades. A score of 85% indicates a high level of proficiency in a subject.
Advanced Percentage Calculations: Going Beyond the Basics
While calculating 9 out of 10 is a simple case, understanding more complex percentage calculations is beneficial. Here are some examples:
1. Finding the Percentage Increase or Decrease:
Calculating percentage change (increase or decrease) involves comparing two values and expressing the difference as a percentage of the original value. The formula is:
[(New Value - Original Value) / Original Value] x 100%
For example, if a product's price increased from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100% = 20%
Conversely, if the price decreased from $60 to $50, the percentage decrease would be:
[(50 - 60) / 60] x 100% = -16.67%
2. Calculating the Original Value Given a Percentage and the Result:
Sometimes, you might know the percentage change and the final value, and you need to calculate the original value. This involves working backward from the formula above.
For example, if a price increased by 15% to $75, the original value can be calculated as:
Original Value = $75 / (1 + 15/100) = $65
3. Calculating Percentage Points vs. Percentage Change:
It's crucial to differentiate between percentage points and percentage change. Percentage points represent the absolute difference between two percentages, while percentage change represents the relative difference.
For example, if an interest rate increased from 2% to 5%, the increase is 3 percentage points (5% - 2% = 3 percentage points), but the percentage change is a 150% increase [(3/2) x 100%].
Mastering Percentages: Tips and Tricks
-
Practice Regularly: The best way to master percentages is through consistent practice. Solve various problems involving different scenarios.
-
Visual Aids: Using visual aids like diagrams or charts can help visualize the proportions represented by percentages.
-
Online Resources: Several online resources offer interactive exercises and tutorials on percentages.
-
Real-World Applications: Relate percentage calculations to real-world situations to improve understanding and retention.
-
Check your work: Double-check your calculations to ensure accuracy and prevent errors.
Conclusion: The Power of Percentages
Understanding percentages is a fundamental skill with widespread applications. From everyday transactions to complex financial and scientific calculations, percentages provide a clear and efficient way to represent proportions, analyze data, and make informed decisions. This detailed guide has not only answered the question "What percent is 9 out of 10?" but has also provided a thorough understanding of percentages and their applications in various contexts. By mastering this essential mathematical concept, you can navigate numerous aspects of life with greater confidence and competence.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Is 9 Out Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.