What Percent Of 10 Is 7
News Co
Mar 26, 2025 · 4 min read
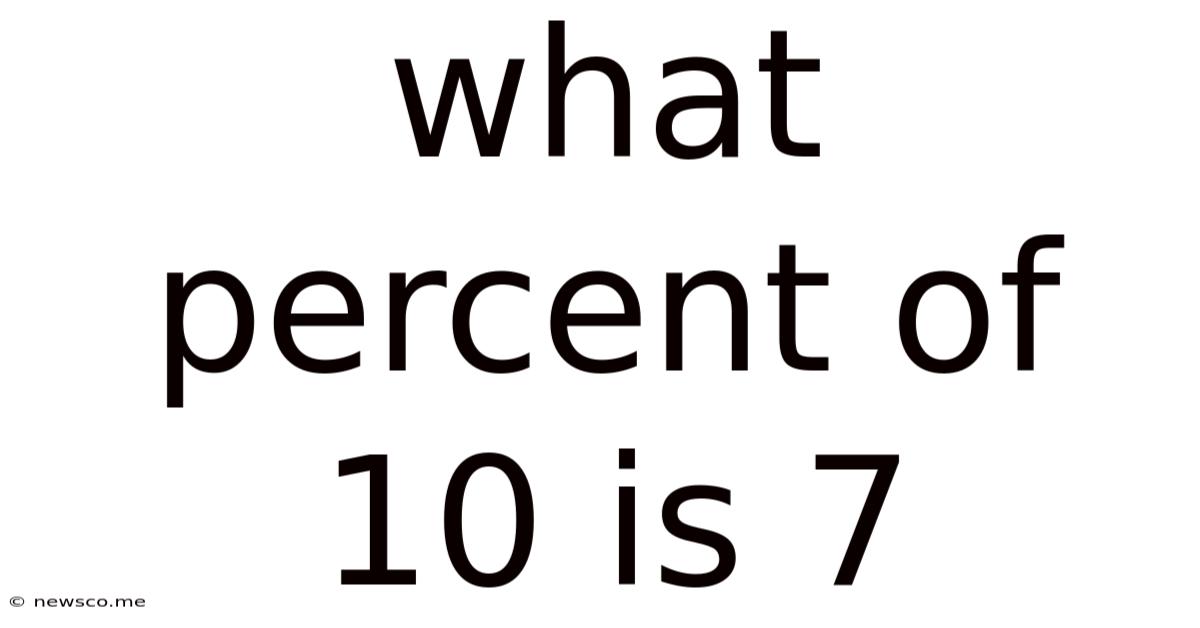
Table of Contents
What Percent of 10 is 7? Understanding Percentages and Their Applications
This seemingly simple question, "What percent of 10 is 7?", opens the door to a broader understanding of percentages, their calculation, and their widespread applications in various fields. While the answer itself is straightforward, the process of arriving at it and the implications of percentage calculations are far-reaching. This article will delve into the solution, explore the underlying mathematical concepts, and illustrate the relevance of percentages in real-world scenarios.
Calculating the Percentage: A Step-by-Step Guide
To determine what percent of 10 is 7, we need to set up a simple equation. Percentages represent parts of a whole, expressed as a fraction of 100. We can express this problem as:
x/100 * 10 = 7
Where 'x' represents the percentage we're trying to find. Let's solve for x:
-
Isolate 'x': Divide both sides of the equation by 10: x/100 = 7/10
-
Simplify the fraction: 7/10 can be expressed as 0.7
-
Solve for 'x': Multiply both sides by 100: x = 0.7 * 100 = 70
Therefore, 7 is 70% of 10.
Understanding the Core Concepts: Fractions, Decimals, and Percentages
The calculation above hinges on the interconnectedness of fractions, decimals, and percentages. These three represent different ways of expressing the same numerical value:
-
Fraction: A fraction shows a part of a whole, expressed as a ratio (e.g., 7/10).
-
Decimal: A decimal represents a fraction using base-10 notation (e.g., 0.7).
-
Percentage: A percentage represents a fraction as parts per hundred (e.g., 70%).
Converting between these forms is crucial for various mathematical operations and problem-solving. Understanding these conversions allows for flexible manipulation of numerical data, making complex calculations more manageable.
Practical Applications of Percentage Calculations
Percentages are ubiquitous, impacting our daily lives in numerous ways. Here are just a few examples:
1. Finance and Budgeting:
-
Interest rates: Banks and financial institutions use percentages to calculate interest on loans, savings accounts, and credit cards. Understanding interest rates is critical for making informed financial decisions.
-
Discounts and sales: Retailers frequently advertise discounts as percentages (e.g., "20% off"). Calculating the actual savings requires understanding percentage calculations.
-
Taxes: Governments levy taxes on income, goods, and services, often expressed as percentages (e.g., sales tax, income tax). Accurate tax calculation necessitates proficiency in percentage computations.
-
Investment returns: Investors track their investment performance using percentages, analyzing gains and losses over time.
2. Science and Statistics:
-
Data analysis: Percentages are frequently used to represent proportions and trends in data sets. Researchers use percentages to summarize findings and draw conclusions.
-
Probability: Probability is often expressed as a percentage, representing the likelihood of an event occurring.
-
Error rates: In scientific experiments and measurements, error rates are often expressed as percentages to quantify the uncertainty associated with results.
3. Everyday Life:
-
Tipping: Calculating tips in restaurants is a common application of percentage calculations.
-
Grading: Grades in schools and universities are often expressed as percentages, reflecting a student's performance.
-
Nutritional information: Food labels show the percentage of daily recommended values for various nutrients.
-
Surveys and polls: Results from surveys and polls are frequently presented as percentages to summarize public opinion.
Beyond the Basics: More Complex Percentage Problems
While calculating "What percent of 10 is 7?" is relatively straightforward, more complex percentage problems require additional steps:
1. Finding the percentage increase or decrease:
Calculating the percentage change between two values involves determining the difference between the values, dividing that difference by the original value, and then multiplying by 100 to express the result as a percentage.
For example, if a price increases from $10 to $12, the percentage increase is calculated as:
((12 - 10) / 10) * 100 = 20%
2. Calculating the original value:
If you know the final value and the percentage increase or decrease, you can work backward to find the original value. This often involves setting up an equation and solving for the unknown variable.
3. Dealing with multiple percentages:
Problems involving consecutive percentage changes (e.g., a 10% increase followed by a 5% decrease) require careful attention to order of operations and the correct application of percentage calculations.
Mastering Percentages: Tips and Resources
Developing a strong understanding of percentages requires consistent practice and a methodical approach. Here are some helpful tips:
-
Practice regularly: Work through various percentage problems to build confidence and fluency.
-
Visual aids: Utilize visual aids like charts and diagrams to represent percentage relationships.
-
Online calculators: Online percentage calculators can be used to check answers and aid in understanding calculations. However, it's crucial to understand the underlying principles to solve problems independently.
-
Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or online communities if you encounter difficulties.
Conclusion: The Significance of Percentage Literacy
The seemingly simple question, "What percent of 10 is 7?", reveals the fundamental importance of understanding percentages. Percentages are not merely abstract mathematical concepts; they are essential tools used across diverse disciplines and in our daily lives. From managing personal finances to interpreting scientific data, proficiency in percentage calculations is a valuable skill that enhances decision-making and problem-solving capabilities. Mastering percentages empowers individuals to navigate the complexities of the modern world with greater confidence and efficiency. The ability to accurately calculate and interpret percentages is a cornerstone of numerical literacy, a skill vital for success in various aspects of life.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 10 Is 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.