What Percent Of 15 Is 10
News Co
Mar 29, 2025 · 5 min read
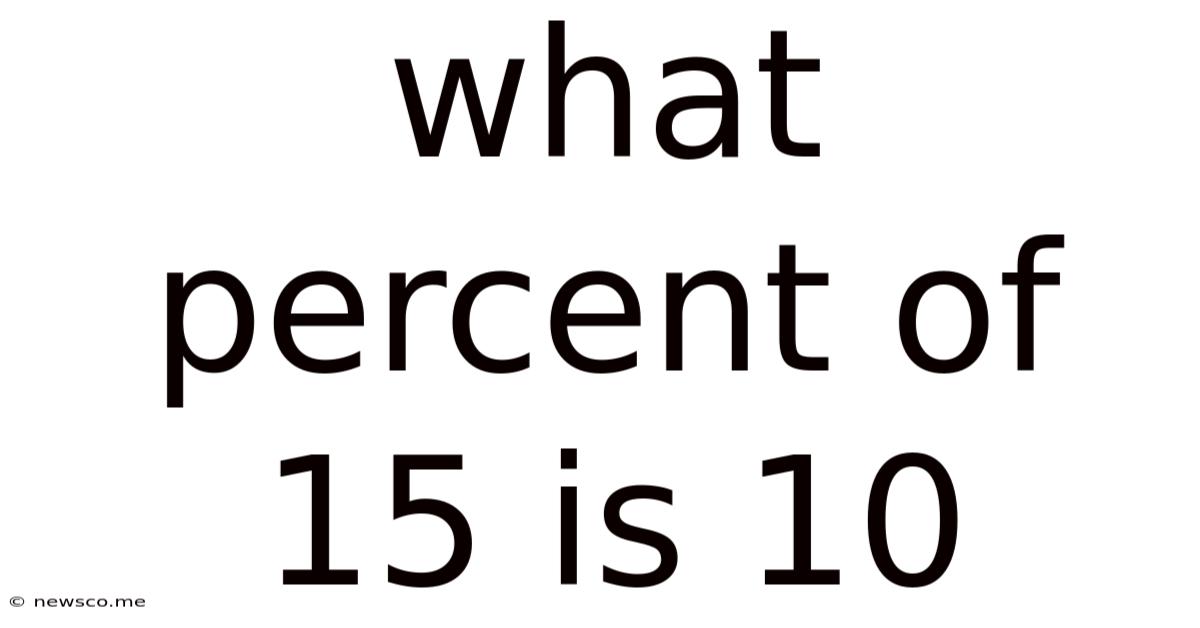
Table of Contents
What Percent of 15 is 10? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "What percent of 15 is 10?", opens the door to a deeper understanding of percentage calculations, a fundamental skill applicable across various fields, from finance and statistics to everyday life. This comprehensive guide will not only answer the question but will also equip you with the knowledge and strategies to tackle similar percentage problems with confidence.
Understanding Percentages
Before diving into the specifics, let's establish a firm grasp on the concept of percentages. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Method 1: Setting up a Proportion
One of the most common and reliable methods for solving percentage problems is setting up a proportion. A proportion is an equation stating that two ratios are equal. In our case, we can set up a proportion as follows:
10/15 = x/100
Where:
- 10 represents the part (the number we're interested in finding the percentage of).
- 15 represents the whole (the total number).
- x represents the unknown percentage we want to find.
- 100 represents the whole in percentage terms (100%).
To solve for x, we cross-multiply:
10 * 100 = 15 * x
1000 = 15x
x = 1000/15
x ≈ 66.67
Therefore, 10 is approximately 66.67% of 15.
Understanding the Proportion: A Deeper Dive
The proportion method allows for a clear visualization of the relationship between the parts and the whole. By setting up the equation 10/15 = x/100, we directly compare the ratio of the part to the whole with the ratio of the percentage to 100%. This approach is particularly helpful in understanding the underlying logic of percentage calculations.
Method 2: Using the Percentage Formula
The percentage formula provides a more direct approach to solving percentage problems. The formula is:
(Part / Whole) * 100 = Percentage
In our problem:
- Part = 10
- Whole = 15
Plugging the values into the formula:
(10 / 15) * 100 = Percentage
(0.6667) * 100 ≈ 66.67%
This method confirms our previous result: 10 is approximately 66.67% of 15.
Advantages of the Percentage Formula
The percentage formula offers a concise and efficient way to calculate percentages. It's particularly useful for quickly solving problems when you already understand the relationship between the part and the whole. This method emphasizes the direct calculation, making it ideal for routine percentage computations.
Method 3: Using Decimal Conversion
This method involves converting the fraction representing the part to the whole into a decimal and then multiplying by 100 to express it as a percentage.
First, express the ratio as a fraction: 10/15
Then, simplify the fraction: 2/3
Convert the fraction to a decimal by dividing the numerator by the denominator: 2 ÷ 3 ≈ 0.6667
Finally, multiply the decimal by 100 to express it as a percentage: 0.6667 * 100 ≈ 66.67%
Therefore, 10 is approximately 66.67% of 15.
Advantages of Decimal Conversion
The decimal conversion method highlights the numerical relationship between the fraction and its percentage equivalent. It is particularly helpful for understanding how fractions translate to percentages, reinforcing the fundamental concept of ratios and proportions. This method’s clarity makes it especially beneficial for beginners.
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in many real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, and profit margins.
- Statistics: Analyzing data sets, representing proportions, and interpreting survey results.
- Shopping: Determining discounts, comparing prices, and understanding sales tax.
- Science: Expressing experimental results, measuring concentrations, and analyzing data.
- Everyday Life: Tipping in restaurants, calculating sale prices, and understanding proportions in recipes.
Advanced Percentage Problems and Strategies
While the problem "What percent of 15 is 10?" is relatively straightforward, more complex percentage problems can arise. Here are some advanced scenarios and strategies to handle them:
- Finding the Whole: If you know the percentage and the part, you can calculate the whole. For example, if 20% of a number is 10, what is the number? You would use the formula: Whole = (Part / Percentage) * 100.
- Finding the Part: If you know the percentage and the whole, you can calculate the part. For example, what is 30% of 50? You would use the formula: Part = (Percentage / 100) * Whole.
- Percentage Increase/Decrease: Calculating percentage changes is crucial in many applications. For example, if a price increases from $100 to $120, the percentage increase is calculated as: [(New Value - Old Value) / Old Value] * 100.
- Compound Interest: Understanding compound interest involves calculating interest on both the principal amount and accumulated interest over time. This requires iterative percentage calculations.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice, the more proficient you'll become. Solve various percentage problems to build your confidence and understanding.
- Utilize Online Calculators (for verification): While calculators are helpful for verification, ensure you understand the underlying principles before relying solely on them.
- Visualize the Problem: Draw diagrams or use real-world analogies to better understand the relationship between the part and the whole.
- Check Your Work: Always double-check your calculations to avoid errors.
Conclusion: Beyond the Numbers
While the answer to "What percent of 15 is 10?" is approximately 66.67%, the true value lies in the understanding gained through the process. Mastering percentage calculations is not merely about solving equations; it's about developing a numerical literacy that empowers you to navigate various aspects of life with confidence and competence. By understanding the different methods, practicing regularly, and applying the knowledge to real-world scenarios, you can unlock the power of percentages and harness their potential in all areas of your endeavors. Remember, the journey to mastering percentages is a process of understanding the underlying principles, not just memorizing formulas. Embrace the challenge, and you will undoubtedly reap the rewards.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 15 Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.