What Percent Of 30 Is 10
News Co
Apr 19, 2025 · 4 min read
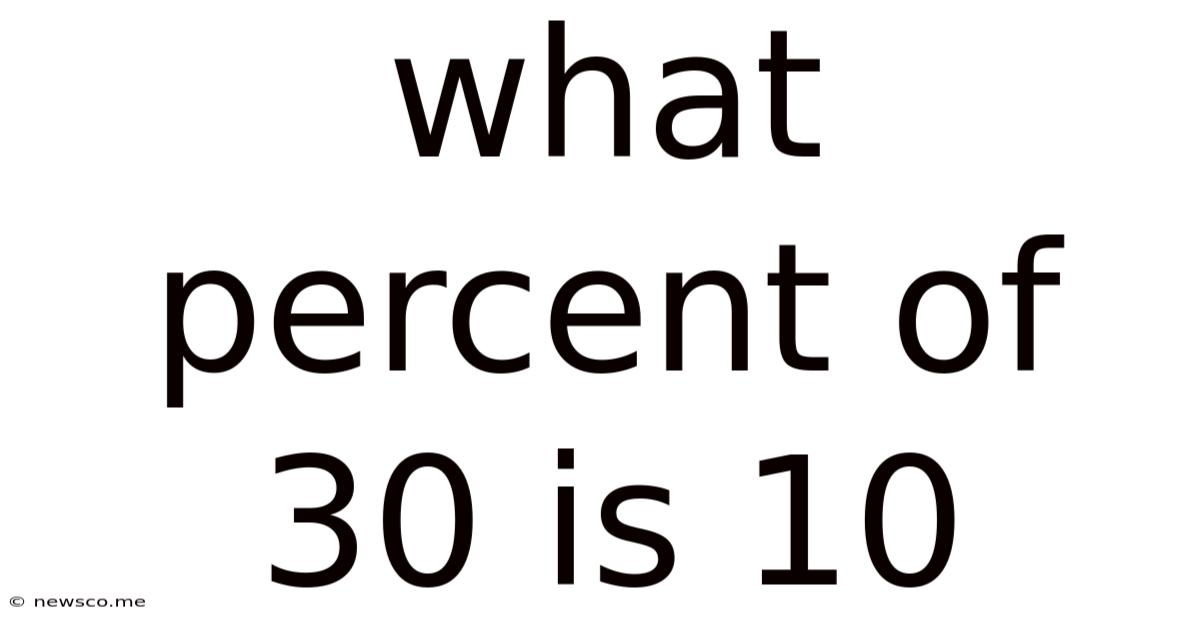
Table of Contents
What Percent of 30 is 10? A Comprehensive Guide to Percentage Calculations
This seemingly simple question – "What percent of 30 is 10?" – opens the door to a deeper understanding of percentages, a fundamental concept in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This article will not only answer this specific question but will also equip you with the knowledge and skills to solve similar percentage problems with confidence. We'll explore multiple approaches, delve into the underlying principles, and provide practical examples to solidify your understanding.
Understanding Percentages
Before we dive into solving the problem, let's establish a solid foundation in understanding percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of 100." For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Key Concepts:
- Part: This represents the specific amount we're interested in (in our case, 10).
- Whole: This represents the total amount (in our case, 30).
- Percentage: This is the fraction of the whole that the part represents, expressed as a number out of 100.
Method 1: Using Proportions
This method uses the power of proportions to solve percentage problems. We can set up a proportion using the given information:
- Part/Whole = Percentage/100
Let's substitute the values from our problem:
- 10/30 = x/100
Where 'x' represents the percentage we want to find.
To solve for 'x,' we cross-multiply:
- 10 * 100 = 30 * x
- 1000 = 30x
Now, divide both sides by 30:
- x = 1000/30
- x ≈ 33.33
Therefore, 10 is approximately 33.33% of 30.
Method 2: Using the Formula
Another common approach involves using a straightforward formula:
- Percentage = (Part/Whole) * 100
Substituting our values:
- Percentage = (10/30) * 100
- Percentage = 0.3333 * 100
- Percentage ≈ 33.33%
This method directly calculates the percentage, offering a more concise solution.
Method 3: Understanding the Relationship
Understanding the underlying relationship between the numbers can also help in solving percentage problems.
We know that 10 is one-third of 30 (30/3 = 10). Since one-third is equivalent to 33.33% (1/3 ≈ 0.3333, and 0.3333 * 100 = 33.33%), we can quickly determine that 10 represents approximately 33.33% of 30. This method offers a quicker solution when dealing with simpler relationships.
Practical Applications of Percentage Calculations
Understanding percentages is crucial for navigating various aspects of daily life:
-
Financial Literacy: Calculating discounts, sales tax, interest rates, tips, and loan repayments all involve percentage calculations. For instance, a 20% discount on a $100 item reduces the price by $20 ($100 * 0.20 = $20).
-
Data Analysis: Percentages are essential in interpreting and presenting data. Analyzing survey results, market trends, and scientific experiments often requires expressing data as percentages to facilitate easy understanding and comparison.
-
Business and Economics: Profit margins, market share, and growth rates are all expressed as percentages, providing essential metrics for businesses to track performance and make informed decisions.
-
Everyday Situations: Calculating the percentage of tasks completed, splitting a bill evenly among friends, understanding nutritional information on food labels – these everyday situations benefit from a solid understanding of percentages.
Advanced Percentage Problems and Techniques
While the problem "What percent of 30 is 10?" is relatively straightforward, percentage problems can become more complex. Here are some advanced scenarios and techniques:
-
Finding the Whole: If you know the percentage and the part, you can find the whole using the formula: Whole = (Part / Percentage) * 100
-
Finding the Part: If you know the percentage and the whole, you can find the part using the formula: Part = (Percentage / 100) * Whole
-
Percentage Change: Calculating percentage increase or decrease is common. The formula for percentage change is: [(New Value - Old Value) / Old Value] * 100
-
Compound Interest: This involves calculating interest on both the principal and accumulated interest. It’s commonly used in finance.
-
Percentage Points: It's important to distinguish between percentage change and percentage points. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
Tips for Solving Percentage Problems
-
Identify the Parts: Clearly define the part and the whole in the problem.
-
Use Consistent Units: Ensure that both the part and the whole use the same units.
-
Check Your Work: Review your calculations to ensure accuracy.
-
Use a Calculator: For more complex calculations, utilize a calculator to avoid errors.
-
Practice Regularly: Solving various percentage problems regularly helps build proficiency and confidence.
Conclusion
Determining "What percent of 30 is 10?" is not just about finding the answer (approximately 33.33%). It’s about grasping the fundamental principles of percentage calculations and appreciating their widespread applications. By understanding the different methods and practicing regularly, you can confidently tackle various percentage problems, enhancing your mathematical skills and improving your ability to interpret and analyze numerical information in diverse contexts. This fundamental understanding empowers you to make informed decisions in numerous aspects of your personal and professional life. Remember to practice, explore different methods, and build your confidence in tackling these seemingly simple yet powerful calculations.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 30 Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.